题目内容
12.定义在R上的函数f(x)满足f(x)=e2x+x2-ax,函数g(x)=f($\frac{x}{2}$)-$\frac{1}{4}$x2+(1-b)x+b(其中a,b为常数),若函数f(x)在x=0处的切线与y轴垂直.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数g(x)的单调区间;
(Ⅲ)若s,t,r满足|s-r|<|t-r|恒成立,则称s比t更靠近,在函数g(x)有极值的前提下,当x≥1时,$\frac{e}{x}$比ex-1+b更靠近,试求b的取值范围.
分析 (Ⅰ)求函数的导数,利用导数的几何意义即可求函数f(x)的解析式;
(Ⅱ)求函数的导数,利用函数单调性和导数之间的关系即可求函数g(x)的单调区间;
(Ⅲ)根据更靠近的定义,构造函数,求函数的导数,利用最值和导数的关系进行求解即可.
解答 解:(Ⅰ)∵f(x)=e2x+x2-ax,∴f′(x)=2e2x+2x-a,
∵函数f(x)在x=0处的切线与y轴垂直.
∴f′(0)=2-a=0,得a=2,
∴f(x)=e2x+x2-2x;
(Ⅱ)g(x)=f($\frac{x}{2}$)-$\frac{1}{4}$x2+(1-b)x+b=ex-b(x-1),
则g′(x)=ex-b,
①若b≤0,g′(x)>0,则g(x)在(-∞,+∞)上为增函数,
②若b>0,由g′(x)>0得x>lnb,由g′(x)<0得x<lnb,
即g(x)在(-∞,lnb)上为减函数,则(lnb,+∞)上为增函数;
(Ⅲ)∵函数g(x)有极值,∴b>0,
由题意知|$\frac{e}{x}$-lnx|<|ex-1+b-lnx|,(※),
设p(x)=$\frac{e}{x}$-lnx,x≥1,q(x)=ex-1+b-lnx,(x≥1),
∵p(x)在[1,+∞)上是减函数,p(e)=0,
∴当1≤x≤e时,p(x)=$\frac{e}{x}$-lnx≥0,
当x>e时,p(x)=$\frac{e}{x}$-lnx<0,
∵q′(x)=ex-1-$\frac{1}{x}$,∴q′(x)在[1,+∞)上为增函数,
∴q′(x)≥q′(1)=0,即q(x)在[1,+∞)上为增函数,
则q(x)≥q(1)=b+1>0,则q(x)=ex-1+b-lnx>0,
①当1≤x≤e时,$\frac{e}{x}$-lnx<ex-1+b-lnx,即b>$\frac{e}{x}$-ex-1,
设m(x)=$\frac{e}{x}$-ex-1,
∵m(x)=$\frac{e}{x}$-ex-1,在[1,e]上为减函数,
∴b>m(1),即b>e-1,
②当x>e时,(※)即lnx-$\frac{e}{x}$<ex-1+b-lnx,即b>-$\frac{e}{x}$+2lnx-ex-1,
设n(x)=-$\frac{e}{x}$+2lnx-ex-1,x>e,
则n′(x)=$\frac{e}{{x}^{2}}$+$\frac{2}{x}$-ex-1,x>e,
则n′(x)在(e,+∞)上为减函数,
∴n′(x)<n′(e),
∵n′(e)=$\frac{3}{e}$-ee-1<0,
∴n(x)在(e,+∞)上为减函数,
n(x)<n(e)=1-ee-1,
则b≥1-ee-1,
综上b>e-1.
点评 本题主要考查不等式恒成立,利用函数单调性最值和导数之间的关系,是解决本题的关键.综合性较强,运算量较大,难度比较大.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
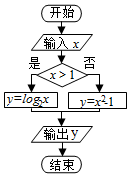
| A. | l | B. | 2 | C. | 3 | D. | 4 |
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
| A. | $\frac{35}{2}$ | B. | 35 | C. | $\frac{25}{2}$ | D. | 25 |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

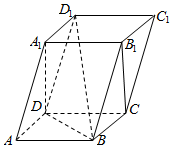 在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.