题目内容
已知函数f(x)=
sin(x-
),f′(x)是f(x)的导函数,若f′(x)=2f(x),求
的值.
| 2 |
| π |
| 4 |
| 3-cos2x |
| cos2x-sinxcosx |
考点:导数的运算
专题:导数的概念及应用
分析:先求出f′(x),由f′(x)=2f(x),求出tanx的值,再去求解.
解答:
解:因为函数f(x)=
sin(x-
),
所以f′(x)=
cos(x-
),
又f′(x)=2f(x),
即
cos(x-
)=2
sin(x-
),
∴tan(x-
)=
,
解得:tanx=3,
cos2x=
=-
,
cos2x=
=
,
sinxcosx=
=
,
∴
=
=-19.
| 2 |
| π |
| 4 |
所以f′(x)=
| 2 |
| π |
| 4 |
又f′(x)=2f(x),
即
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
∴tan(x-
| π |
| 4 |
| 1 |
| 2 |
解得:tanx=3,
cos2x=
| 1-tan2x |
| 1+tan2x |
| 4 |
| 5 |
cos2x=
| 1+cos2x |
| 2 |
| 1 |
| 10 |
sinxcosx=
| tanx |
| 1+tan2x |
| 3 |
| 10 |
∴
| 3-cos2x |
| cos2x-sinxcosx |
3-(-
| ||||
|
点评:本题主要考查函数的导数的求法,万能公式的应用,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设函数f(x)=
,若方程f(x)=a恰有一实根,则a的取值范围为( )
|
| A、(-∞,0]∪(1,+∞) | ||
| B、(-∞,0)∪[1,+∞) | ||
| C、(-∞,0)∪(1,+∞) | ||
D、(-∞,0)∪(
|
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
A、ln 2+
| ||
B、ln 2-
| ||
C、ln 2-
| ||
D、ln 2-
|
已知F1、F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,过点F1且斜率为k的直线与双曲线的右支交于点M,若点M在x轴上的射影恰好是右焦点F2,且
<k<
,则双曲线离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
| 4 |
| 3 |
| A、(1,2) |
| B、(1,3) |
| C、(3,+∞) |
| D、(2,3) |
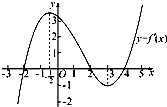 如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数的图象如图所示,给出下列判断: