题目内容
已知点Q(5,4),若动点P(x,y)满足
,则PQ的最小值为( )
|
A、
| ||||
B、
| ||||
| C、5 | ||||
| D、以上都不对 |
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:由约束条件作出P点的区域,求出BQ连线的斜率,求得的斜率小于1,可知过Q点作直线x+y-2=0的垂线,垂足在直线上B的下方,由此可知当P在B点处PQ的距离最小.
解答:
解:由约束条件足
,得P(x,y)所在区域如图,
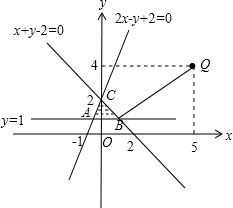
联立
,得B(1,1),
∵kQB=
=
,过Q点与直线x+y-2=0垂直的直线的斜率为1,
∴过Q点作直线x+y-2=0的垂线,垂足在直线上B的下方,
∴可行域内的点P为点B时PQ的值最小,最小值为
=5.
故选:C.
|

联立
|
∵kQB=
| 4-1 |
| 5-1 |
| 3 |
| 4 |
∴过Q点作直线x+y-2=0的垂线,垂足在直线上B的下方,
∴可行域内的点P为点B时PQ的值最小,最小值为
| (5-1)2+(4-1)2 |
故选:C.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,关键是找出使PQ值最小的点,是中档题.

练习册系列答案
相关题目
若A(-2,3)、B(3,-2)、C(
,m﹚三点在同一直线上,则m的值为( )
| 1 |
| 2 |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
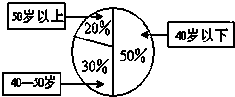 某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )
某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )