题目内容
已知函数f(x)=x,g(x)为偶函数,且当x≥0时,g(x)=x2-2x.记max{a,b}=
.给出下列关于函数F(x)=max{f(x),g(x)}(x∈R)的说法:
①当x≥3时,F(x)=x2-2x;
②函数F(x)为奇函数;
③函数F(x)在[-1,1]上为增函数;
④函数F(x)的最小值为-1,无最大值.
其中正确的是( )
|
①当x≥3时,F(x)=x2-2x;
②函数F(x)为奇函数;
③函数F(x)在[-1,1]上为增函数;
④函数F(x)的最小值为-1,无最大值.
其中正确的是( )
| A、①②④ | B、①③④ |
| C、①③ | D、②④ |
考点:命题的真假判断与应用
专题:函数的性质及应用
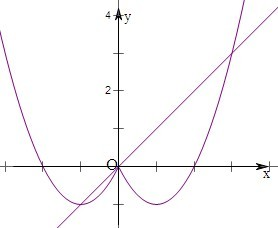
分析:可结合图象写出F(x)的解析式,然后结合F(x)的图象判断函数F(x)的奇偶性和单调性,从而判断②③的正确,最后结合图象分段求函数F(x)的最值.
解答:
解:因为函数f(x)=x,g(x)为偶函数,且当x≥0时,g(x)=x2-2x,所以g(x)=x2-2|x|,
F(x)=
,所以当x≥3时,F(x)=x2-2x,即①对;
因为F(x)的图象不关于原点对称,所以函数F(x)不为奇函数,即②错;
由图象知函数F(x)在[-1,3]上是增函数,所以在[-1,1]上是增函数,即③对;
由图象易知函数F(x)的最小值为F(-1)=-1,无最大值.即④对.
故选:B
F(x)=
|
因为F(x)的图象不关于原点对称,所以函数F(x)不为奇函数,即②错;
由图象知函数F(x)在[-1,3]上是增函数,所以在[-1,1]上是增函数,即③对;
由图象易知函数F(x)的最小值为F(-1)=-1,无最大值.即④对.
故选:B

点评:本题主要考查函数的两个重要性质--奇偶性和单调性,考查数学上数形结合这一重要方法,是一道中档题.

练习册系列答案
相关题目
某射击俱乐部四名运动员甲、乙、丙、丁在选拔赛中所得的平均环数
及其方差s2如表所示,若从中选送一人参加决赛,则最佳人选是( )
. |
| x |
| 甲 | 乙 | 丙 | 丁 | |||
|
9.1 | 9.3 | 9.3 | 9.2 | ||
| s2 | 5.7 | 6.2 | 5.7 | 6.4 |
| A、甲 | B、乙 | C、丙 | D、丁 |
已知sin(
+x)=
(
<x<
),则式子
的值为( )
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
| π |
| 2 |
| cos2x | ||
cos(
|
A、-
| ||
B、
| ||
C、
| ||
D、-
|
方程sinx=-cos80°的解集是( )
| A、{X|X=k•180°+10°,k∈z} |
| B、{x|x=k•360°+10°,k∈z} |
| C、{x|x=k•180°±10°,k∈z} |
| D、{x|x=k•180°-(-1)k•10°,k∈z} |
已知点Q(5,4),若动点P(x,y)满足
,则PQ的最小值为( )
|
A、
| ||||
B、
| ||||
| C、5 | ||||
| D、以上都不对 |