题目内容
判断下列函数的奇偶性．
（1）y=
+
；
（2）y=sin（
+
）．
（1）y=
| 1-cosx |
| cosx-1 |
（2）y=sin（
| 3x |
| 4 |
| 3π |
| 2 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：先求出函数的定义域，判断定义域是否关于原点对称，再验证f（-x）与f（x）的关系，进而判断函数的奇偶性．
解答：
解：（1）要使函数有意义，必有cosx=1，即x=2kπ，k∈Z，
又y=0，
故y=
+
既是奇函数又是偶函数；
（2）f（x）y=sin（
+
）的定义域为R，
又f（x）=y=sin（
+
）=-cos
，
f（-x）=-cos
=cos
=f(x)，
故y=sin（
+
）是偶函数．
故答案为：（1）既是奇函数又是偶函数
（2）偶函数
又y=0，
故y=
| 1-cosx |
| cosx-1 |
（2）f（x）y=sin（
| 3x |
| 4 |
| 3π |
| 2 |
又f（x）=y=sin（
| 3x |
| 4 |
| 3π |
| 2 |
| 3x |
| 4 |
f（-x）=-cos
| 3(-x) |
| 4 |
| 3x |
| 4 |
故y=sin（
| 3x |
| 4 |
| 3π |
| 2 |
故答案为：（1）既是奇函数又是偶函数
（2）偶函数
点评：判断一个函数是否具有奇偶性，先求出定义域，判断定义域是否关于原点对称，若不关于原点对称函数不具有奇偶性；若关于原点对称，再验证f（-x）与f（x）的关系．
练习册系列答案
相关题目
过抛物线 y2=4x 的焦点作直线交抛物线于A（x1，y1）B（x2，y2）两点，如果x1+x2=10，那么|AB|=（ ）
| A、11 | B、12 | C、13 | D、14 |
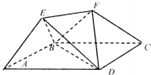如图，底面ABCD是边长为2的菱形，且∠BAD=