题目内容
已知α,β∈[0,
],则sin(α-β)+2sin(α+β)的最大值为 .
| π |
| 4 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:设f(α)=sin(α-β)+2sin(α+β),α,β∈[0,
]可求f'(α)>0,则f(α)单调递增,最大值即为f(
),故可解得sin(α-β)+2sin(α+β)的最大值为
.
| π |
| 4 |
| π |
| 4 |
| 5 |
解答:
解:设f(α)=sin(α-β)+2sin(α+β),α,β∈[0,
]
f(α)=sinαcosβ-cosαsinβ+2sinαcosβ+2cosαsinβ=3sinαcosβ+cosαsinβ
f'(α)=3cosαcosβ-sinαsinβ=2cosαcosβ+cos(α+β)
∵α,β∈[0,
],
∴f'(α)>0,f(α)单调递增
∴f(α)最大值=f(
)=3×
×cosβ+
×sinβ=
(3cosβ+sinβ)=
sin(β+t),其中tant=3,
∴sin(α-β)+2sin(α+β)的最大值为
.
故答案为:
.
| π |
| 4 |
f(α)=sinαcosβ-cosαsinβ+2sinαcosβ+2cosαsinβ=3sinαcosβ+cosαsinβ
f'(α)=3cosαcosβ-sinαsinβ=2cosαcosβ+cos(α+β)
∵α,β∈[0,
| π |
| 4 |
∴f'(α)>0,f(α)单调递增
∴f(α)最大值=f(
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 5 |
∴sin(α-β)+2sin(α+β)的最大值为
| 5 |
故答案为:
| 5 |
点评:本题主要考察了两角和与差的正弦函数,复合函数的单调性,属于中档题.

练习册系列答案
相关题目
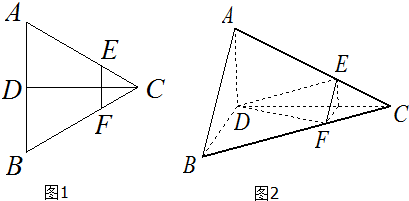
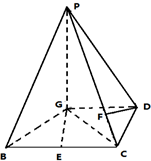 已知四棱锥P-GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=
已知四棱锥P-GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=