题目内容
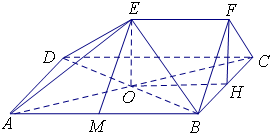
 如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=| 3 |
(1)求证:AB⊥平面BCF;
(2)求直线AE与平面BDE所成角的正切值.
考点:直线与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)先证明出四边形EMBF是平行四边形,推断出EM∥FB,EM=FB.进而在Rt△BFC中求得EM,在△AEM中,根据边长推断出AM2+EM2=3=AE2,进而证明出AM⊥EM.然后证明出四边形ABCD是正方形,进而推断出AB⊥BC.最后通过线面垂直的判定定理证明出AB⊥平面BCF.
(2)先证明出∠AEO是直线AE与平面BDE所成的角,进而在Rt△AOE中,求得tan∠AEO.
(2)先证明出∠AEO是直线AE与平面BDE所成的角,进而在Rt△AOE中,求得tan∠AEO.
解答:
 (1)证明:取AB的中点M,连接EM,则AM=MB=1,
(1)证明:取AB的中点M,连接EM,则AM=MB=1,
∵EF∥平面ABCD,EF?平面ABEF,平面ABCD∩平面ABEF=AB,
∴EF∥AB,即EF∥MB.
∵EF=MB=1
∴四边形EMBF是平行四边形.
∴EM∥FB,EM=FB.
在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB=
.
∴EM=
.
在△AEM中,AE=
,AM=1,EM=
,
∴AM2+EM2=3=AE2,
∴AM⊥EM.
∴AM⊥FB,即AB⊥FB.
∵四边形ABCD是正方形,
∴AB⊥BC.
∵FB∩BC=B,FB?平面BCF,BC?平面BCF,
∴AB⊥平面BCF.
(2)连接AC,AC与BD相交于点O,则点O是AC的中点,
取BC的中点H,连接OH,EO,FH,
则OH∥AB,OH=
AB=1.
由(1)知EF∥AB,且EF=
AB,
∴EF∥OH,且EF=OH.
∴四边形EOHF是平行四边形.
∴E0∥FH,且EO=FH=1.
由(1)知AB⊥平面BCF,又FH?平面BCF,
∴FH⊥AB,
∵FH⊥BC,AB∩BC=B,FH?平面ABCD,BC平面ABCD,
∴FH⊥平面ABCD.
∴E0⊥平面ABCD.
∵AO?平面ABCD,
∴EO⊥AO.
∵AO⊥BD,EO∩BD=O,EO?平面EBD,BD平面EBD,
∴AO⊥平面EBD.
∴∠AEO是直线AE与平面BDE所成的角.
在Rt△AOE中,tan∠AEO=
=
.
∴直线AE与平面BDE所成角的正切值为
.
 (1)证明:取AB的中点M,连接EM,则AM=MB=1,
(1)证明:取AB的中点M,连接EM,则AM=MB=1,∵EF∥平面ABCD,EF?平面ABEF,平面ABCD∩平面ABEF=AB,
∴EF∥AB,即EF∥MB.
∵EF=MB=1
∴四边形EMBF是平行四边形.
∴EM∥FB,EM=FB.
在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB=
| 2 |
∴EM=
| 2 |
在△AEM中,AE=
| 3 |
| 2 |
∴AM2+EM2=3=AE2,
∴AM⊥EM.
∴AM⊥FB,即AB⊥FB.
∵四边形ABCD是正方形,
∴AB⊥BC.
∵FB∩BC=B,FB?平面BCF,BC?平面BCF,
∴AB⊥平面BCF.
(2)连接AC,AC与BD相交于点O,则点O是AC的中点,
取BC的中点H,连接OH,EO,FH,
则OH∥AB,OH=
| 1 |
| 2 |
由(1)知EF∥AB,且EF=
| 1 |
| 2 |
∴EF∥OH,且EF=OH.
∴四边形EOHF是平行四边形.
∴E0∥FH,且EO=FH=1.
由(1)知AB⊥平面BCF,又FH?平面BCF,
∴FH⊥AB,
∵FH⊥BC,AB∩BC=B,FH?平面ABCD,BC平面ABCD,
∴FH⊥平面ABCD.
∴E0⊥平面ABCD.
∵AO?平面ABCD,
∴EO⊥AO.
∵AO⊥BD,EO∩BD=O,EO?平面EBD,BD平面EBD,
∴AO⊥平面EBD.
∴∠AEO是直线AE与平面BDE所成的角.
在Rt△AOE中,tan∠AEO=
| AO |
| EO |
| 2 |
∴直线AE与平面BDE所成角的正切值为
| 2 |
点评:本题主要考查了线面垂直的判定定理的应用,二面角的求法.解题的关键是找到二面角的平面角.

练习册系列答案
相关题目
 边长为2的菱形ABCD中,∠A=60°,沿BD折成直二面角,过点A作PA⊥平面ABC,且AP=2
边长为2的菱形ABCD中,∠A=60°,沿BD折成直二面角,过点A作PA⊥平面ABC,且AP=2 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ. 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.