题目内容
1.已知定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=(x-a)2-a2,且对x∈R,恒有f(x+1)≥f(x),则实数a的取值范围为(-∞,$\frac{1}{4}$].分析 根据函数奇偶性的性质求出函数f(x)的解析式,讨论a的取值,作出函数f(x)的图象,利用图象平移以及数形结合进行求解即可.
解答 解:∵定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=(x-a)2-a2,
∴若x<0,则-x>0,
则f(-x)=(-x-a)2-a2=-f(x),
即f(x)=-(x+a)2+a2,x<0,
若a≤0,则f(x)=$\left\{\begin{array}{l}{(x-a)^{2}-{a}^{2}}&{x≥0}\\{-(x+a)^{2}+{a}^{2}}&{x<0}\end{array}\right.$在定义域上为增函数,恒有f(x+1)≥f(x)成立,
当a>0时,函数f(x)的图象如图:
∵f(x+1)的图象可以函数是由函数f(x)的图象向左平移1个单位得到的,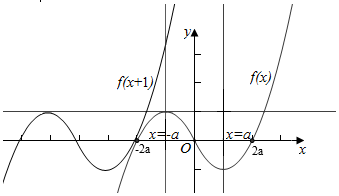
需要函数f(x)的图象至少向左平移2a-(-2a)=4a个单位才能满足f(x+1)≥f(x)恒成立,
则4a≤1,即0<a≤$\frac{1}{4}$,
综上a≤$\frac{1}{4}$,
故答案为:(-∞,$\frac{1}{4}$]
点评 本题主要考查不等式恒成立问题,利用函数奇偶性求出函数的解析式,以及利用分类讨论和数形结合以及图象平移关系是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
9.计算∫01x2dx值属于区间( )
| A. | (0,$\frac{1}{2}$) | B. | [$\frac{1}{2}$,1) | C. | [1,$\frac{3}{2}$) | D. | [$\frac{3}{2}$,2) |
6.设一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上10,得到一组新数据,则所得新数据的平均数和方差分别是( )
| A. | 12.8 3.6 | B. | 2.8 13.6 | C. | 12.8 13.6 | D. | 13.6 12.8 |
10.已知$\frac{\overline z}{3+i}$=1+i,则复数z在复平面上对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.下面关于复数$z=\frac{2}{1+i}$的四个命题:p1:|z|=2,${p_2}:{z^2}=2i$,p3:z的共轭复数为1+i,p4:z在复平面内对应点位于第四象限.其中真命题为( )
| A. | p2、p3 | B. | p1、p4 | C. | p2、p4 | D. | p3、p4 |
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E在B1D1上,且ED1=2B1E,AC与BD交于点O.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E在B1D1上,且ED1=2B1E,AC与BD交于点O.