题目内容
已知a、b、c成等差数列且公差d≠0,求证:
、
、
不可能成等差数列.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
考点:等差关系的确定
专题:反证法,等差数列与等比数列
分析:命题是否定形式的命题的证明一般采用反证法证明.
解答:
证明:假设
、
、
成等差数列,
-
=
-
即
=
,∴
=
又∵a,b,c成等差数列,且公差d≠0,
∴a-b=b-c≠0.∴a=c,
这与已知数列a,b,c的公差d≠0,a≠c相矛盾,
所以数列
、
、
不可能成等差数列.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| b |
| 1 |
| a |
| 1 |
| c |
| 1 |
| b |
| a-b |
| ab |
| b-c |
| bc |
| a-b |
| a |
| b-c |
| c |
又∵a,b,c成等差数列,且公差d≠0,
∴a-b=b-c≠0.∴a=c,
这与已知数列a,b,c的公差d≠0,a≠c相矛盾,
所以数列
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
点评:本题考查了反证法证明否定性命题.
反证法是一种间接证法,一般地假设命题不成立,推出与假设矛盾,或与某个真命题矛盾,从而判定为假,推出为真的方法叫做反证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法.
用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论.
反证法是一种间接证法,一般地假设命题不成立,推出与假设矛盾,或与某个真命题矛盾,从而判定为假,推出为真的方法叫做反证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法.
用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论.

练习册系列答案
相关题目
下列命题错误的是( )
A、若
| ||||||||
B、若
| ||||||||
C、当m∈R时,恒有m(
| ||||||||
D、|
|
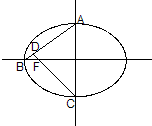 已知如图,椭圆的离心率为
已知如图,椭圆的离心率为| 1 |
| 2 |
A、-3
| ||
B、3-
| ||
C、3
| ||
D、3+
|