题目内容
若函数f(x)的定义域是R,且对?x,y∈R,都有f(x+y)=f(x)+f(y)成立.
(1)试判断f(x)的奇偶性;
(2)若当x>0时,f(x)>0,判断函数的单调性;
(3)若f(8)=4,求f(-
)的值.
(1)试判断f(x)的奇偶性;
(2)若当x>0时,f(x)>0,判断函数的单调性;
(3)若f(8)=4,求f(-
| 1 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)令x=y=0,则可得f(0)=0;再令y=-x,即可证明f(x)是奇函数.
(2)设x1<x2,由已知可得f(x2-x1)>0,再利用f(x+y)=f(x)+f(y)及增函数的定义即可证明.
(3)利用赋值法,得到f(8)=f(4)+f(4)=2f(4)=4f(2)=8f(1)=16f(
)=4,再利用函数奇函数,故求出答案
(2)设x1<x2,由已知可得f(x2-x1)>0,再利用f(x+y)=f(x)+f(y)及增函数的定义即可证明.
(3)利用赋值法,得到f(8)=f(4)+f(4)=2f(4)=4f(2)=8f(1)=16f(
| 1 |
| 2 |
解答:
证明:(1)函数f(x)为奇函数,理由如下
由f(x+y)=f(x)+f(y),
令x=y=0,
∴f(0)=f(0)+f(0)
即f(0)=0
令y=-x,得f(x-x)=f(x)+f(-x)
即f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),
即函数y=f(x)是奇函数
(2)函数y=f(x)是在上为增函数,理由如下,
设x1<x2,则x2-x1>0,
∵当x>0时,f(x)>0,
∴f(x2-x1)>0,
∴f(x2)=f(x2-x1+x1)=f(x2-x1)+f(x1)>f(x1)
∴函数y=f(x)是在上为增函数,
(3)∵f(8)=4,
∴f(8)=f(4)+f(4)=2f(4)=4f(2)=8f(1)=16f(
)=4,
∴f(
)=
,
又函数y=f(x)是奇函数,
∴f(-
)=-f(
)=-
,
由f(x+y)=f(x)+f(y),
令x=y=0,
∴f(0)=f(0)+f(0)
即f(0)=0
令y=-x,得f(x-x)=f(x)+f(-x)
即f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),
即函数y=f(x)是奇函数
(2)函数y=f(x)是在上为增函数,理由如下,
设x1<x2,则x2-x1>0,
∵当x>0时,f(x)>0,
∴f(x2-x1)>0,
∴f(x2)=f(x2-x1+x1)=f(x2-x1)+f(x1)>f(x1)
∴函数y=f(x)是在上为增函数,
(3)∵f(8)=4,
∴f(8)=f(4)+f(4)=2f(4)=4f(2)=8f(1)=16f(
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
| 1 |
| 4 |
又函数y=f(x)是奇函数,
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查了抽象函数的奇偶性和单调性,深刻理解函数奇偶性和单调性的定义及充分利用已知条件是解决问题的关键,属于中档题

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
以下现象是随机现象的是( )
| A、标准大气压下,水加热到100℃,必会沸腾 |
| B、走到十字路口,遇到红灯 |
| C、长和宽分别为a、b的矩形,其面积为a×b |
| D、实系数一次方程必有一实根 |
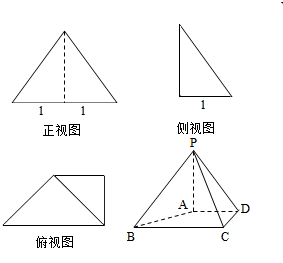 已知四棱锥P-ABCD的三视图如图所示,△PBC为正三角形.
已知四棱锥P-ABCD的三视图如图所示,△PBC为正三角形.