题目内容
已知函数f(x)=alnx-
x+
-1.
(1)求函数f(x)的单调区间;
(2)若a=1,设g(x)=-x2+2bx-4,且满足对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥f(x2) 恒成立,求实数b的取值范围.
| 1 |
| 4 |
| 3a2 |
| 4x |
(1)求函数f(x)的单调区间;
(2)若a=1,设g(x)=-x2+2bx-4,且满足对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥f(x2) 恒成立,求实数b的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)f(x)=alnx-
x+
-1的定义域是(0,+∞),f′(x)=-
,由此利用导数性质能求出函数f(x)的单调递区间.
(2)若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,问题等价于f(x)min≥g(x)max,由此利用导数性质能求出实数b的取值范围.
| 1 |
| 4 |
| 3a2 |
| 4x |
| (x-a)(x-3a) |
| 4x2 |
(2)若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,问题等价于f(x)min≥g(x)max,由此利用导数性质能求出实数b的取值范围.
解答:
解:(1)f(x)=alnx-
x+
-1的定义域是(0,+∞),f′(x)=
-
-
=-
=-
,…(2分)
①当a>0时,函数f(x)的单调递增区间是(a,3a);
单调递减区间是(0,a),(3a,+∞).
②当a≤0时,函数f(x)在(0,+∞)单调递减.…(5分)
(2)若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,
问题等价于f(x)min≥g(x)max,
当a=1时,f(x)=lnx-
x+
-1
由(1)知,在(0,2)上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,
∴f(x)min=f(1)=-
.…(7分)
g(x)=-x2+2bx-4,x∈[1,2],
当b<1时,g(x)max=g(1)=2b-5,
当1≤b≤2时,g(x)max=g(b)=b2-4;
当b>2时,g(x)max=g(2)=4b-8;
问题等价于
,或
,或
.…(10分)
解得b<1或1≤b≤
或b∈∅.…(11分)
即b≤
,
∴实数b的取值范围是(-∞,
].…(12分)
| 1 |
| 4 |
| 3a2 |
| 4x |
| a |
| x |
| 1 |
| 4 |
| 3a2 |
| 4x2 |
| x2-4ax+3a2 |
| 4x2 |
| (x-a)(x-3a) |
| 4x2 |
①当a>0时,函数f(x)的单调递增区间是(a,3a);
单调递减区间是(0,a),(3a,+∞).
②当a≤0时,函数f(x)在(0,+∞)单调递减.…(5分)
(2)若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,
问题等价于f(x)min≥g(x)max,
当a=1时,f(x)=lnx-
| 1 |
| 4 |
| 3 |
| 4x |
由(1)知,在(0,2)上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,
∴f(x)min=f(1)=-
| 1 |
| 2 |
g(x)=-x2+2bx-4,x∈[1,2],
当b<1时,g(x)max=g(1)=2b-5,
当1≤b≤2时,g(x)max=g(b)=b2-4;
当b>2时,g(x)max=g(2)=4b-8;
问题等价于
|
|
|
解得b<1或1≤b≤
| ||
| 2 |
即b≤
| ||
| 2 |
∴实数b的取值范围是(-∞,
| ||
| 2 |
点评:本题考查函数的单调区间的求法,考查实数的取值范围的求法,解题时要认真审题,注意构造法、分类讨论思想和导数性质的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 设圆(x-2)2+(y-2)2=4的切线l与两坐标轴交于点A(a,0),B(0,b),ab≠0.
设圆(x-2)2+(y-2)2=4的切线l与两坐标轴交于点A(a,0),B(0,b),ab≠0.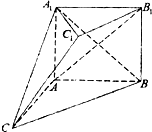 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=