题目内容
已知函数g(x)=x2+ln(x+a),其中a为常数.
(1)讨论函数g(x)的单调性;
(2)若g(x)存在两个极值点x1,x2,求证:无论实数a取什么值都有
>g(
).
(1)讨论函数g(x)的单调性;
(2)若g(x)存在两个极值点x1,x2,求证:无论实数a取什么值都有
| g(x1)+g(x2) |
| 2 |
| x1+x2 |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:(1)利用求导法则求出函数g(x)的导函数,把导函数解析式通分化简,分4a2-8≤0,或4a2-8>0两种情况讨论函数的单调性;
(2)当a>
时,函数g(x)在(
,+∞)或(-a,
)上单调递增,在(
,
)上单调递减;
=
=
a2-
-
ln2,g(
)=g(-
)=
a2+ln
;令f(a)=
a2-lna+
ln2-
,从而得证.
(2)当a>
| 2 |
-a+
| ||
| 2 |
-a-
| ||
| 2 |
-a-
| ||
| 2 |
-a+
| ||
| 2 |
| g(x1)+g(x2) |
| 2 |
| x12+ln(x1+a)+x22+ln(x2+a) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| a |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵g(x)=x2+ln(x+a),
∴函数的定义域为(-a,+∞)
∴g′(x)=2x+
,
令2x+
>0,
2x2+2ax+1>0,
当4a2-8≤0时,即-
≤a≤
时,g′(x)≥0,即函数g(x)在(-a,+∞)单调递增,
当4a2-8>0时,即a>
,或a<-
时,
令g′(x)=0,解得x=
,或x=
,
①若a>
,
当g′(x)>0时,即x>
,或-a<x<
,函数g(x)单调递增,
当g′(x)<0时,即
<x<
,函数g(x)单调递减,
②若a<-
,g′(x)>0,即函数g(x)在(-a,+∞)单调递增,
综上所述:当a≤
时,即函数g(x)在(-a,+∞)单调递增,
当a>
时,函数g(x)在(
,+∞)或(-a,
)上单调递增,
在(
,
)上单调递减,
(2)由(1)可知,当a>
时,函数g(x)在(
,+∞)或(-a,
)上单调递增,
在(
,
)上单调递减,
x1+x2=-a;x1•x2=
,
=
=
a2-
-
ln2,
g(
)=g(-
)=
a2+ln
;
故
-g(
)
=(
a2-
-
ln2)-(
a2+ln
)
=
a2-lna+
ln2-
;
令f(a)=
a2-lna+
ln2-
,
则f′(a)=
a-
=
,
∵a>
,∴
>0;
∴f(a)=
a2-lna+
ln2-
在(
,+∞)上增函数,
且f(
)=0,
故
a2-lna+
ln2-
>0,
故无论实数a取什么值都有
>g(
).
∴函数的定义域为(-a,+∞)
∴g′(x)=2x+
| 1 |
| x+a |
令2x+
| 1 |
| x+a |
2x2+2ax+1>0,
当4a2-8≤0时,即-
| 2 |
| 2 |
当4a2-8>0时,即a>
| 2 |
| 2 |
令g′(x)=0,解得x=
-a+
| ||
| 2 |
-a-
| ||
| 2 |
①若a>
| 2 |
当g′(x)>0时,即x>
-a+
| ||
| 2 |
-a-
| ||
| 2 |
当g′(x)<0时,即
-a-
| ||
| 2 |
-a+
| ||
| 2 |
②若a<-
| 2 |
综上所述:当a≤
| 2 |
当a>
| 2 |
-a+
| ||
| 2 |
-a-
| ||
| 2 |
在(
-a-
| ||
| 2 |
-a+
| ||
| 2 |
(2)由(1)可知,当a>
| 2 |
-a+
| ||
| 2 |
-a-
| ||
| 2 |
在(
-a-
| ||
| 2 |
-a+
| ||
| 2 |
x1+x2=-a;x1•x2=
| 1 |
| 2 |
| g(x1)+g(x2) |
| 2 |
| x12+ln(x1+a)+x22+ln(x2+a) |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
g(
| x1+x2 |
| 2 |
| a |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
故
| g(x1)+g(x2) |
| 2 |
| x1+x2 |
| 2 |
=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
令f(a)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
则f′(a)=
| 1 |
| 2 |
| 1 |
| a |
| a2-2 |
| 2a |
∵a>
| 2 |
| a2-2 |
| 2a |
∴f(a)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
且f(
| 2 |
故
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
故无论实数a取什么值都有
| g(x1)+g(x2) |
| 2 |
| x1+x2 |
| 2 |
点评:本题考查了导数的综合应用,同时考查了恒成立问题,属于难题.

练习册系列答案
相关题目
命题“若△ABC不是等腰三角形,则它的任何两个内角不相等”的逆否命题是 ( )
| A、“若△ABC是等腰三角形,则它的任何两个内角相等” |
| B、“若△ABC任何两个内角不相等,则它不是等腰三角形” |
| C、“若△ABC有两个内角相等,则它是等腰三角形” |
| D、“若△ABC任何两个角相等,则它是等腰三角形” |
具有性质:f(
)=-f(x)的函数,我们称为满足“倒负”交换的函数,则下列函数:①y=x-
;②y=x+
;③y=lnx;④y=
中所有满足“到负”交换的函数是( )
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
|
| A、①③ | B、②④ | C、①④ | D、①③④ |
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),然后把图象向左平移
个单位,则所得图形对应的函数解析式为( )
| π |
| 8 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(
|
 如图是某粮食烘干设备的简易图,它是由两个完全一样的四棱锥P1-ABCD与P2-ABCD组成,四边形ABCD是边长为a的正方形,O1、O2分别是BC、AD的中点,P1O2⊥面ABCD,P2O1⊥面ABCD,且P1O2=P2O1=a,设备工作时,粮食从两个四棱两端的非公共部分流入烘干设备,烘干后粮食自动流到公共部分,要使这个粮食烘干设备一次烘干粮食的体积不小于45个单位体积,求a的最小值.
如图是某粮食烘干设备的简易图,它是由两个完全一样的四棱锥P1-ABCD与P2-ABCD组成,四边形ABCD是边长为a的正方形,O1、O2分别是BC、AD的中点,P1O2⊥面ABCD,P2O1⊥面ABCD,且P1O2=P2O1=a,设备工作时,粮食从两个四棱两端的非公共部分流入烘干设备,烘干后粮食自动流到公共部分,要使这个粮食烘干设备一次烘干粮食的体积不小于45个单位体积,求a的最小值.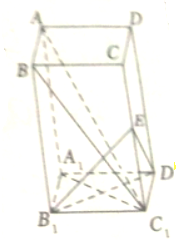 在长方体ABCD-A1B1C1D1中,E∈CC1,B1E⊥BC1,AB=CD,求证:AC1⊥面B1ED1.
在长方体ABCD-A1B1C1D1中,E∈CC1,B1E⊥BC1,AB=CD,求证:AC1⊥面B1ED1.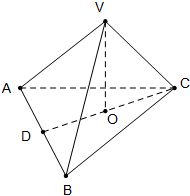 如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证:
如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证: