题目内容
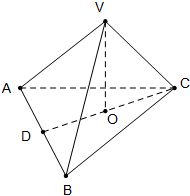 如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证:
如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证:(1)AB⊥平面VDC;
(2)AB⊥CD.
考点:直线与平面垂直的判定,直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:(1)连接VD,由VA=VB,AD=BD可得VD⊥AB,又由VO⊥平面ABC,得VO⊥AB,从而AB⊥平面VDO,由C在直线DO上,即可得证;
(2)由(1)得AB⊥平面VDC,从而由CD?平面VDC,可得AB⊥CD.
(2)由(1)得AB⊥平面VDC,从而由CD?平面VDC,可得AB⊥CD.
解答:
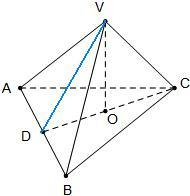 证明:(1)连接VD,从而∵VA=VB,AD=BD
证明:(1)连接VD,从而∵VA=VB,AD=BD
∴VD⊥AB
∵VO⊥平面ABC,∴VO⊥AB
∴AB⊥平面VDO,
∵C在直线DO上,
∴AB⊥平面VDC;
(2)由(1)得AB⊥平面VDC;
∵CD?平面VDC
∴AB⊥CD.
 证明:(1)连接VD,从而∵VA=VB,AD=BD
证明:(1)连接VD,从而∵VA=VB,AD=BD∴VD⊥AB
∵VO⊥平面ABC,∴VO⊥AB
∴AB⊥平面VDO,
∵C在直线DO上,
∴AB⊥平面VDC;
(2)由(1)得AB⊥平面VDC;
∵CD?平面VDC
∴AB⊥CD.
点评:本题主要考察了直线与平面垂直的判定,直线与平面垂直的性质,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为 ( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不确定 |
4个人排成一排,甲不能站在两边,则不同的排法种数有( )种.
| A、12 | B、16 | C、8 | D、20 |
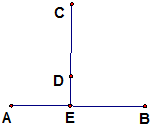 如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.
如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.