题目内容
在△ABC中,∠A=30°,|AB|=2,S△ABC=
.若以A,B为焦点的椭圆经过点C,则该椭圆的离心率e= .
| 3 |
考点:椭圆的简单性质
专题:解三角形,圆锥曲线的定义、性质与方程
分析:利用正弦定理、余弦定理,以A,B为焦点的椭圆经过点C,求出2a=|AC|+|BC|=2
+2,2c=|AB|=2,即可求出椭圆的离心率.
| 3 |
解答:
解,∠A=30°,|AB|=2,S△ABC=
.
∴
×2×|AC|×
=
,
∴|AC|=2
,
∴|BC|2=22+(2
)2-2×2×2
×
=4,
∴|BC|=2,
∵以A,B为焦点的椭圆经过点C,
∴2a=|AC|+|BC|=2
+2,2c=2,
∴e=
=
=
=
.
故答案为:
.
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴|AC|=2
| 3 |
∴|BC|2=22+(2
| 3 |
| 3 |
| ||
| 2 |
∴|BC|=2,
∵以A,B为焦点的椭圆经过点C,
∴2a=|AC|+|BC|=2
| 3 |
∴e=
| c |
| a |
| 2c |
| 2a |
| 2 | ||
2
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查椭圆的性质及应用,解题时要注意的定义的正确运用,属于基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
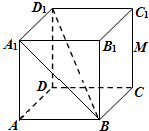
 如图建立空间直角坐标系,已知正方体的棱长为2,
如图建立空间直角坐标系,已知正方体的棱长为2,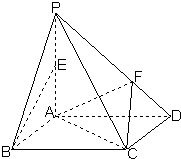 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,E为PA的中点.
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,E为PA的中点.