题目内容
如图建立空间直角坐标系，已知正方体的棱长为2，（1）求正方体各顶点的坐标；
（2）求A1C的长度．
考点：空间两点间的距离公式,空间中的点的坐标
专题：计算题,空间位置关系与距离
分析：（1）利用空间直角坐标系中点的坐标表示方法，可得结论；
（2）
=（2，2，-2），即可求A1C的长度．
（2）
| A1C |
解答：
解：（1）由正方体的棱长为2，得AA（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），A1（0，0，2），B1（2，0，2），C1（2，2，2），D1（0，2，2）；
（2）
=（2，2，-2），
∴A1C的长度=|
|=
=2
．
（2）
| A1C |
∴A1C的长度=|
| A1C |
| 4+4+4 |
| 3 |
点评：由空间向量的坐标表示得到空间直角坐标系中点的坐标表示，这是解本题的思路．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
已知F1，F2为双曲线C：
-y2=1的左、右焦点，点P在C上，|PF1|=2|PF2|，则cos∠F1PF2=（ ）
| x | 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
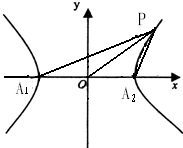如图，P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、（0，
| ||
B、（0，
| ||
C、（0，
| ||
D、（0，
|
已知A，B是两个相互独立事件，P（A），P（B）分别表示它们发生的概率，则1-P（A）P（B）是下列哪个事件的概率（ ）
| A、事件A，B同时发生 |
| B、事件A，B至少有一个发生 |
| C、事件A，B至多有一个发生 |
| D、事件A，B都不发生 |
已知一个几何体的正（主）视图与侧（左）视图均为长等于2的正三角形，俯视图如图所示，在俯视图中，半圆的直径与等腰直角三角形的斜边长均为2，则该几何体的体积为（ ）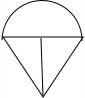
A、
| ||||
B、
| ||||
C、
| ||||
D、
|