题目内容
18.若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”,现从0,1,2,3,4,5,6,7,这个数字中任取3个,组成无重复数字的三位数,其中“伞数”有91个(用数字作答)分析 根据题意,分2种情况讨论:①、取出的3个数字中不含0,先在1,2,3,4,5,6,7中任取3个数,再分析每种取法的“伞数”数目,由分步计数原理可得此时的“伞数”数目,②、取出的3个数字中含有0,同①可得其“伞数”数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、取出的3个数字中不含0,
先在1,2,3,4,5,6,7中任取3个数,有C73=35种取法,
把最大的数放在十位,剩下的2个数全排列,放在百位、个位,有A22=2种情况,
则此时一共有35×2=70个“伞数”,
②、取出的3个数字中含有0,
需要在1,2,3,4,5,6,7中任取2个数,有C72=21种取法,
把最大的数放在十位,0放在个位,剩下的数放在百位,有1种情况,
则此时一共有21×1=21个“伞数”,
则一共有70+21=91个“伞数”,
故答案为:91.
点评 本题考查排列、组合的应用,注意0不能在百位,需要对0进行分类讨论.

练习册系列答案
相关题目
3.已知命题p∧q是假命题,p∨q是真命题,则下列命题一定是真命题的是( )
| A. | q | B. | (?p)∧(?q) | C. | p | D. | (?p)∨(?q) |
7.已知递增数列{an}对任意n∈N*均满足an∈N*,aan=3n,记${b_n}={a_{2•{3^{n-1}}}}$(n∈N*),则数列{bn}的前n项和等于( )
| A. | 2n+n | B. | 2n+1-1 | C. | $\frac{{{3^{n+1}}-3n}}{2}$ | D. | $\frac{{{3^{n+1}}-3}}{2}$ |
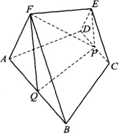 如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.
如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.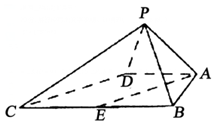 如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.