题目内容
在△OAB中,已知O(0,0),A(8,0),B(0,6),△OAB的内切圆的方程为(x-2)2+(x-2)2=4,点P是圆上一点.
(1)求点P到直线l:4x+3y+11=0的距离的最大值和最小值;
(2)若S=|PO|2+|PA|2+|PB|2,求S的最大值和最小值.
(1)求点P到直线l:4x+3y+11=0的距离的最大值和最小值;
(2)若S=|PO|2+|PA|2+|PB|2,求S的最大值和最小值.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)求出圆的圆心与半径,利用圆心与直线的距离公式求出距离,即可求出点P到直线l:3x+4y+3=0距离的最值;
(2)设出P的坐标的参数形式,利用S=|PO|2+|PA|2+|PB|2,求出表达式,利用圆的参数方程即可求S的最大值与最小值.
(2)设出P的坐标的参数形式,利用S=|PO|2+|PA|2+|PB|2,求出表达式,利用圆的参数方程即可求S的最大值与最小值.
解答:
解:(1)∵△OAB的内切圆的方程为(x-2)2+(x-2)2=4,
∴圆心M(2,2),r=2,
∴M到直线l的距离 d=
d=
=
=5,
∴P(x,y)到直线l的距离最大值为d+r=5+2=7,最小值为d-r=5-2=3.
(2)设P(x,y),则点P满足
,
则M=|PO|2+|PA|2+|PB|2=(2+2cosθ)2+(2+2sinθ)2+(2cosθ-6)2+(2+2sinθ)2+(2+2cosθ)2+(2sinθ-4)2]
=80-8cosθ,
∴当cosθ=1时,S取得最小值为S=80-8=72,
当cosθ=-1时,S取得最大值为S=80+8=88.
∴圆心M(2,2),r=2,
∴M到直线l的距离
 d=
d=| |4×2+3×2+11| | ||
|
| 25 |
| 5 |
∴P(x,y)到直线l的距离最大值为d+r=5+2=7,最小值为d-r=5-2=3.
(2)设P(x,y),则点P满足
|
则M=|PO|2+|PA|2+|PB|2=(2+2cosθ)2+(2+2sinθ)2+(2cosθ-6)2+(2+2sinθ)2+(2+2cosθ)2+(2sinθ-4)2]
=80-8cosθ,
∴当cosθ=1时,S取得最小值为S=80-8=72,
当cosθ=-1时,S取得最大值为S=80+8=88.
点评:本题主要考查点到直线的距离公式的应用,圆与直线的关系,圆的参数方程,三角函数的应用,考查计算能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
一双曲线焦点的坐标,离心率分别为(±5,0)、
,则它的共轭双曲线的焦点坐标、离心率分别分别是( )
| 3 |
| 2 |
A、(0,±5),
| ||||||
B、(0,±5),
| ||||||
C、(0,±
| ||||||
D、(0,±
|
某几何体的立体图如图所示,该几何体的三视图不可能是( )
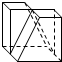

A、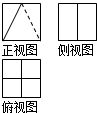 |
B、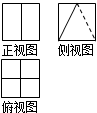 |
C、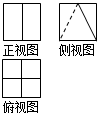 |
D、 |