题目内容
已知f(α)=
.
(1)化简f(α);
(2)若α是第四象限角,且cos(
-α)=
,求f(α)的值.
sin(π-α)cos(2π-α)sin(-α+
| ||
cos(-π-α)cos(-α+
|
(1)化简f(α);
(2)若α是第四象限角,且cos(
| 3π |
| 2 |
| 1 |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)由条件利用诱导公式化简可得所给式子的值,可得结果.
(2)由条件利用同角三角函数的基本关系求得f(α)的值.
(2)由条件利用同角三角函数的基本关系求得f(α)的值.
解答:
解:(1)f(α)=
=
=-cosα.
(2)若α是第四象限角,且cos(
-α)=-sinα=
,∴sinα=-
,
∴f(α)=-cosα=-
=-
.
sin(π-α)cos(2π-α)sin(-α+
| ||
cos(-π-α)cos(-α+
|
| sinα•cosα•(-cosα) |
| -cosα•(-sinα) |
(2)若α是第四象限角,且cos(
| 3π |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
∴f(α)=-cosα=-
| 1-sin2α |
2
| ||
| 3 |
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,要特别注意符号的选取,这是解题的易错点,属于基础题.

练习册系列答案
相关题目
已知A、B是抛物线y2=4p上不同的两点,且直线AB的倾斜角为锐角,F为抛物线的焦点,且
=-4
,则直线AB的斜率为( )
| FA |
| FB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)和g(x)的定义如表:
则方程g(f(x))=x的解集是( )
| x | 1 | 2 | 3 | x | 1 | 2 | 3 | |
| f(x) | 2 | 3 | 1 | g(x) | 3 | 2 | 1 |
| A、Φ | B、{3} |
| C、{2} | D、{1} |
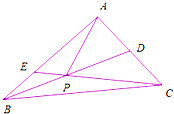 如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若
如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若