题目内容
19. 机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心出发,先沿北偏西θ(sinθ=$\frac{12}{13}$)方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B,C都在圆上,则在以线段BC中点为坐标原点O,正东方向为x轴正方向,正北方向为y轴正方向的直角坐标系中,圆的标准方程为x2+(y-9)2=225.
机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心出发,先沿北偏西θ(sinθ=$\frac{12}{13}$)方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B,C都在圆上,则在以线段BC中点为坐标原点O,正东方向为x轴正方向,正北方向为y轴正方向的直角坐标系中,圆的标准方程为x2+(y-9)2=225.
分析 由已知求解三角形得OT、BT的长度,以BC所在直线为x轴,以BC得垂直平分线为y轴距离平面直角坐标系,可得圆T的圆心坐标,代入圆的标准方程得答案.
解答 解:如图所示:sinθ=$\frac{12}{13}$,TA=13,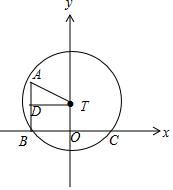
∴cos∠ATD=sinθ=$\frac{12}{13}$,TD=TA•cos∠ATD=13×$\frac{12}{13}$=12,
AD=TA•sin∠ATD=13×$\frac{5}{13}$=5,
∴BD=14-AD=9,∴TB2=TD2+BD2=144+81=225,
以BC所在直线为x轴,以BC得垂直平分线为y轴距离平面直角坐标系,
则T(0,9),
故圆T的方程为 x2+(y-9)2=225,
故答案为:x2+(y-9)2=225.
点评 本题主要考查直角三角形中的边角关系,求圆的标准方程,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
14.已知等差数列{an},S3=6,a9+a11+a13=60,则S13的值为( )
| A. | 66 | B. | 42 | C. | 169 | D. | 156 |
4.如图是一个几何体的三视图,则该几何体的体积是( )

| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 4 |
8.下列说法正确的是( )
| A. | 当f′(x0)=0时,f(x0)为f(x)的极大值 | B. | 当f′(x0)=0时,f(x0)为f(x)的极小值 | ||
| C. | 当f′(x0)=0时,f(x0)为f(x)的极值 | D. | 当f(x0)为f(x)的极值时,f′(x0)=0 |
9.把67化为二进制数为( )
| A. | 1 100 001(2) | B. | 1 000 011(2) | C. | 110 000(2) | D. | 1 000 111(2) |