题目内容
(本题满分16分)在平面直角坐标系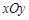 中,已知圆
中,已知圆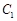 :
: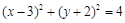 ,圆
,圆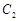 :
: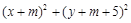
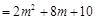 (
(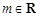 ,且
,且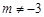 ).
).
(1)设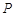 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆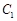 与圆
与圆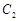 的一条切线,切点分别为
的一条切线,切点分别为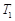 、
、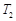 ,使得
,使得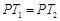 ,试求出所有满足条件的点
,试求出所有满足条件的点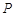 的坐标;
的坐标;
(2)若斜率为正数的直线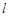 平分圆
平分圆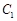 ,求证:直线
,求证:直线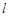 与圆
与圆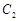 总相交.
总相交.
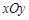 中,已知圆
中,已知圆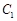 :
: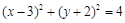 ,圆
,圆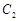 :
: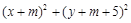
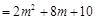 (
(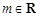 ,且
,且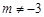 ).
).(1)设
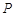 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆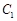 与圆
与圆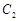 的一条切线,切点分别为
的一条切线,切点分别为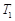 、
、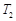 ,使得
,使得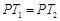 ,试求出所有满足条件的点
,试求出所有满足条件的点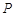 的坐标;
的坐标;(2)若斜率为正数的直线
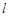 平分圆
平分圆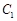 ,求证:直线
,求证:直线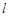 与圆
与圆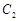 总相交.
总相交.(1) 或
或 (2)见解析
(2)见解析
 或
或 (2)见解析
(2)见解析(1)设点 的坐标为
的坐标为 ,圆
,圆 与圆
与圆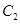 的半径分别为
的半径分别为 ,
,
由题意得 ,
,
即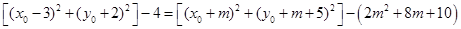 3分
3分
化简得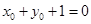 , 5分
, 5分
因为 为坐标轴上的点,
为坐标轴上的点,
所以点 的坐标为
的坐标为 或
或 . 7分
. 7分
(2)依题意可设直线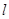 的方程为:
的方程为: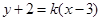 ,
, ,化简得
,化简得 ,
,
则圆心 到直线
到直线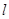 的距离为
的距离为 ,
,
又圆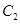 的半径为
的半径为 , 10分
, 10分
所以,“直线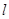 与圆
与圆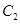 总相交”等价于
总相交”等价于
“ ,且
,且 ,
,
 ,
,
即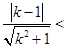
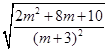 ①,” 12分
①,” 12分
记 ,整理得
,整理得 ,
,
当 时,
时, ;
;
当 时,判别式
时,判别式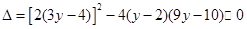 ,解得
,解得 ;
;
综上得 ,
, 的最小值为1, 14分
的最小值为1, 14分
所以,①式


 ,即证. 16分
,即证. 16分
【命题意图】本题考查直线与圆知识 ,意在考查运算求解能力,数学综合论证能力.
 的坐标为
的坐标为 ,圆
,圆 与圆
与圆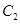 的半径分别为
的半径分别为 ,
,由题意得
 ,
,即
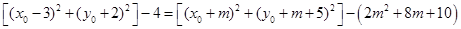 3分
3分化简得
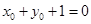 , 5分
, 5分因为
 为坐标轴上的点,
为坐标轴上的点,所以点
 的坐标为
的坐标为 或
或 . 7分
. 7分(2)依题意可设直线
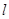 的方程为:
的方程为: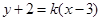 ,
, ,化简得
,化简得 ,
, 则圆心
 到直线
到直线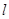 的距离为
的距离为 ,
,又圆
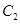 的半径为
的半径为 , 10分
, 10分所以,“直线
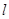 与圆
与圆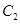 总相交”等价于
总相交”等价于“
 ,且
,且 ,
,
 ,
, 即
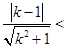
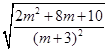 ①,” 12分
①,” 12分记
 ,整理得
,整理得 ,
,当
 时,
时, ;
;当
 时,判别式
时,判别式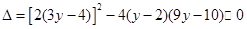 ,解得
,解得 ;
;综上得
 ,
, 的最小值为1, 14分
的最小值为1, 14分所以,①式



 ,即证. 16分
,即证. 16分【命题意图】本题考查直线与圆知识 ,意在考查运算求解能力,数学综合论证能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 ,若在圆
,若在圆 上存在点
上存在点 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )



 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )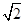 ,1+2
,1+2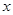 +4
+4 +8=0上的动点,PA、PB是圆
+8=0上的动点,PA、PB是圆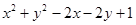 =0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
=0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 . ,则两圆的外公切线段长等于 .
,则两圆的外公切线段长等于 . 和圆:
和圆: 交于A、B两点,则AB的垂直平分线的方程是( ).
交于A、B两点,则AB的垂直平分线的方程是( ). B.
B. C.
C.  D.
D.
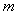 ,直线
,直线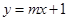 与圆
与圆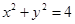 的位置关系一定是( )
的位置关系一定是( ) 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )

