题目内容
已知P是直线3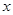 +4
+4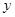 +8=0上的动点,PA、PB是圆
+8=0上的动点,PA、PB是圆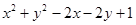 =0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
=0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
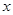 +4
+4 +8=0上的动点,PA、PB是圆
+8=0上的动点,PA、PB是圆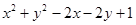 =0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
=0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
试题分析:圆C:
 即
即 ,表示以C(1,1)为圆心,以1为半径的圆.由于四边形PACB面积等于 2×
,表示以C(1,1)为圆心,以1为半径的圆.由于四边形PACB面积等于 2× PA×AC=PA,而 PA=
PA×AC=PA,而 PA= ,故当PC最小时,四边形PACB面积最小.又PC的最小值等于圆心C到直线l:3x+4y+8="0" 的距离d,而d=
,故当PC最小时,四边形PACB面积最小.又PC的最小值等于圆心C到直线l:3x+4y+8="0" 的距离d,而d= =3,故四边形PACB面积的最小的最小值为
=3,故四边形PACB面积的最小的最小值为
 =2
=2 ,故选B.
,故选B.
练习册系列答案
相关题目
 中,已知圆
中,已知圆 :
: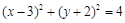 ,圆
,圆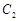 :
: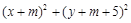
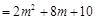 (
(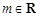 ,且
,且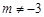 ).
).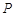 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆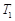 、
、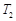 ,使得
,使得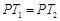 ,试求出所有满足条件的点
,试求出所有满足条件的点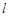 平分圆
平分圆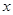 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为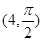 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为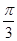 ,圆C的半径为4.
,圆C的半径为4.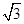 ,则直线l的方程为( )
,则直线l的方程为( )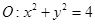 上任取一点
上任取一点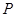 ,过点
,过点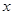 轴的垂线段
轴的垂线段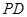 ,
,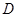 为垂足.设
为垂足.设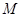 为线段
为线段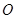 上运动时,求点
上运动时,求点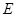 的方程;
的方程;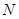 ,试判断直线
,试判断直线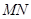 与轨迹
与轨迹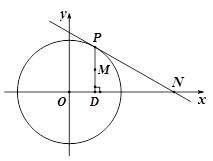
 是直线
是直线
 上一动点,
上一动点, 是圆C:
是圆C: 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形 的最小面积是2,则
的最小面积是2,则 的值为?
的值为?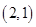 作圆
作圆 的弦,其中最短的弦长为 .
的弦,其中最短的弦长为 .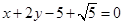 被圆
被圆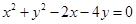 截得的弦长为 ( )
截得的弦长为 ( )