题目内容
(1)已知l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,求直线l1的方程;
(2)求经过两条直线l1:x-2y+4=0和l2:x+y-2=0的交点P且与直线l3:3x-4y+5=0垂直的直线l的方程.
(2)求经过两条直线l1:x-2y+4=0和l2:x+y-2=0的交点P且与直线l3:3x-4y+5=0垂直的直线l的方程.
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:(1)由题意求出要求直线的斜率,代入直线方程的点斜式得答案;
(2)联立方程组求得交点坐标,求出要求直线的斜率,由直线方程的斜截式得答案.
(2)联立方程组求得交点坐标,求出要求直线的斜率,由直线方程的斜截式得答案.
解答:
解:(1)当l1,l2间的距离最大时,两直线与AB垂直,
∵kAB=
=2,则kl1=-
,
∴直线l1的方程为y-1=-
(x-1),即x+2y-3=0;
(2)联立
,解得
.
∴两条直线l1:x-2y+4=0和l2:x+y-2=0的交点P(0,2),
∵直线l3:3x-4y+5=0的斜率为
,
∴所求直线的斜率为-
.
∴所求直线方程为y=-
x+2.
∵kAB=
| 1-(-1) |
| 1-0 |
| 1 |
| 2 |
∴直线l1的方程为y-1=-
| 1 |
| 2 |
(2)联立
|
|
∴两条直线l1:x-2y+4=0和l2:x+y-2=0的交点P(0,2),
∵直线l3:3x-4y+5=0的斜率为
| 3 |
| 4 |
∴所求直线的斜率为-
| 4 |
| 3 |
∴所求直线方程为y=-
| 4 |
| 3 |
点评:本题考查了直线的一般式方程与直线的垂直关系,是基础的计算题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况为5,6,7,8,9,10.用简单随机抽样的方法从这6名学生中抽取2名,并将他们的得分组成一个样本,则该样本的平均数与总体平均数之差的绝对值不超过0.5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列等式成立的是( )
| A、lg(xy)=lgx+lgy | ||
B、log2
| ||
| C、logax2=2logax(a>0,且a≠1) | ||
| D、lnx3=3lnx |
下列函数中,在定义域内既是奇函数,又是增函数是( )
| A、y=sinx |
| B、y=x3-x |
| C、y=2x |
| D、y=x3 |
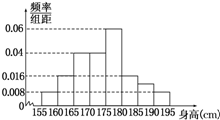 从某学校高三年级800名学生中随机抽取50名测量身高,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…第八组[190,195],如图是按上述分组方法得到的频率分布直方图.
从某学校高三年级800名学生中随机抽取50名测量身高,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…第八组[190,195],如图是按上述分组方法得到的频率分布直方图.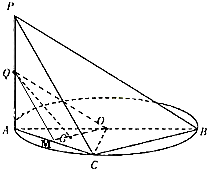 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.