题目内容
若变量x,y满足约束条件
,则ω=
的取值范围是( )
|
| y-1 |
| x+1 |
A、[-
| ||||
B、[-
| ||||
C、[-1,
| ||||
D、[-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,ω=
的几何意义为动点(x,y)到点(-1,1)的斜率,利用数形结合即可得到结论.
| y-1 |
| x+1 |
解答:
 解:ω=
解:ω=
的几何意义为动点P(x,y)到点D(-1,1)的斜率,
作出不等式组对应的平面区域如图(阴影部分):
由图象可知当P位于点A(1,0)时,AD的斜率最小,
此时ω=
=
=-
,
当过D的直线和2x-y-2=0平行时,此时斜率最大为2,但取不到,
故ω∈[-
,2),
故选:A.
 解:ω=
解:ω=| y-1 |
| x+1 |
作出不等式组对应的平面区域如图(阴影部分):
由图象可知当P位于点A(1,0)时,AD的斜率最小,
此时ω=
| y-1 |
| x+1 |
| -1 |
| 1+1 |
| 1 |
| 2 |
当过D的直线和2x-y-2=0平行时,此时斜率最大为2,但取不到,
故ω∈[-
| 1 |
| 2 |
故选:A.
点评:本题主要考查线性规划的基本应用,利用目标函数的几何意义以及斜率公式是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
y=
x2-ln(2x-3)的单调递减区间为( )
| 1 |
| 2 |
A、(-∞,-
| ||
| B、(2,+∞) | ||
C、(
| ||
D、(
|
已知O是△ABC内部一点,且3
+
+
=
,
•
=6,∠BAC=60°,则△OBC的面积为( )
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
实数x,y满足条件
,则z=x-2y的最小值为( )
|
| A、5 | B、-3 | C、2 | D、以上都不对 |
过点P(12,0)且与y轴相切于原点的圆的方程为( )
| A、(x+6)2+y2=36 |
| B、x2+(y+6)2=36 |
| C、(x-6)2+y2=36 |
| D、x2+(y-6)2=36 |
椭圆
+
=1的离心率是( )
| x2 |
| 4 |
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将相邻的5个不同编号的房间安排给5个工作人员临时休息,假定每个人可以选择任一房间,且选择各个房间是等可能的,若恰有2个房间无人选择且这2个房间不相邻,则不同的安排方式的总数为( )
| A、60 | B、90 |
| C、150 | D、900 |
不等式组
,表示的平面区域为Ω,直线y=kx-1与区域Ω有公共点,则实数k的取值范围为( )
|
| A、(0,3] |
| B、[-1,1] |
| C、(-∞,3] |
| D、[3,+∞) |
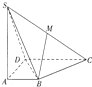 四棱锥S-ABCD中,SA⊥平面ABCD,底面四边形ABCD为直角梯形,AB∥CD,AD⊥DC,SA=AD=DC=2,AB=1.
四棱锥S-ABCD中,SA⊥平面ABCD,底面四边形ABCD为直角梯形,AB∥CD,AD⊥DC,SA=AD=DC=2,AB=1.