题目内容
y=sin(ωx+ϕ)(ω>0,|ϕ|<
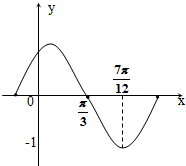
)的图象的一部分图形如图所示,则函数的解析式为( )
| π |
| 2 |

A、y=sin(x+
| ||
B、y=sin(x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答:
解:由函数的图象可得A=1,
=
•
=
-
,求得ω=2.
再根据五点法作图可得2×
+φ=π,求得φ=
,故函数的解析式为 y=sin(2x+
),
故选:C.
| T |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再根据五点法作图可得2×
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故选:C.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=loga(ax2-x+3)在[2,4]上是增函数,则实数a的取值范围是( )
| A、a>1 | ||||
| B、0<a<1或a>1 | ||||
C、
| ||||
D、
|
在1,2,3,4四个数中,任取两个不同的数,其和大于积的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知U={2,3,4,5},M={3,4,5},N={2,4,5},则( )
| A、M∩N={4,3} |
| B、M∪N=U |
| C、{∁UN}∪M=U |
| D、(∁UM)∪N=M |
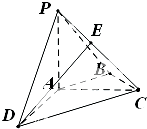 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=