题目内容
若函数f(x)=2x2-mx+3的单调增区间是[-2,+∞),则f(1)= .
考点:二次函数的性质
专题:函数的性质及应用
分析:由函数f(x)=2x2-mx+3的单调增区间是[-2,+∞),可得:
=-2,求出函数的解析式后,将x=1代入可得答案.
| m |
| 4 |
解答:
解:∵函数f(x)=2x2-mx+3的单调增区间是[-2,+∞),
∴
=-2,
解得m=-8,
故f(x)=2x2+8x+3,
故f(1)=13,
故答案为:13
∴
| m |
| 4 |
解得m=-8,
故f(x)=2x2+8x+3,
故f(1)=13,
故答案为:13
点评:本题考查的知识点是二次函数的性质,其中熟练掌握二次函数的单调性是解答的关键.

练习册系列答案
相关题目
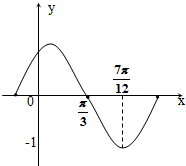
y=sin(ωx+ϕ)(ω>0,|ϕ|<
)的图象的一部分图形如图所示,则函数的解析式为( )
| π |
| 2 |

A、y=sin(x+
| ||
B、y=sin(x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
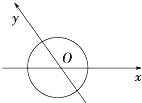 如图,Ox、Oy是平面内相交成120°的两条数轴,
如图,Ox、Oy是平面内相交成120°的两条数轴,