题目内容
在1,2,3,4四个数中,任取两个不同的数,其和大于积的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:所有的取法有
=6种方法,用列举法求得满足条件的取法有3种,由此求得所求事件的概率.
| C | 2 4 |
解答:
解:在数字1、2、3、4四个数中,任取两个不同的数,共有
=6种方法,
其中,满足其和大于积的取法有:(1,2)、(1,3)、(1,4)共三种,
故其和大于积的概率是
=
,
故选:C.
| C | 2 4 |
其中,满足其和大于积的取法有:(1,2)、(1,3)、(1,4)共三种,
故其和大于积的概率是
| 3 |
| 6 |
| 1 |
| 2 |
故选:C.
点评:本题考查古典概型及其概率计算公式的应用,属于基础题.

练习册系列答案
相关题目
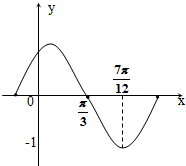
y=sin(ωx+ϕ)(ω>0,|ϕ|<
)的图象的一部分图形如图所示,则函数的解析式为( )
| π |
| 2 |

A、y=sin(x+
| ||
B、y=sin(x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
设a>0,b>0,则下列叙述正确的是( )
| A、若lna-2b>lnb-2a,则a>b |
| B、若lna-2b>lnb-2a,则a<b |
| C、若lna-2a>lnb-2b,则a>b |
| D、若lna-2a>lnb-2b,则a<b |
已知函数f(x)是奇函数,当x>0时,f(x)=-x(1+2x);当x<0时,f(x)等于( )
| A、-x(1+2x) |
| B、x(1+2x) |
| C、x(1-2x) |
| D、-x(1-2x) |