题目内容
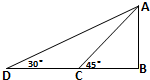如图，D，C，B在地平面同一直线上，DC=10m，从D，C两地测得A点的仰角分别为30°和45°，则A点离地面的高AB等于（ ）| A、10m | ||
B、5
| ||
C、5（
| ||
D、5（
|
考点：解三角形的实际应用
专题：解三角形
分析：分别在Rt△ABC和Rt△ABD中用AB表示出BC，BD，作差建立方程求得AB．
解答：
解：在Rt△ABC中，BC=AB，
在Rt△ABD中，BD=
AB，
又BD-BC=10，
∴
AB-AB=10，
AB=5（
+1）（m），
故A点离地面的高AB为5（
+1）m，
故选D．
在Rt△ABD中，BD=
| 3 |
又BD-BC=10，
∴
| 3 |
AB=5（
| 3 |
故A点离地面的高AB为5（
| 3 |
故选D．
点评：本题主要考查了解三角形的实际应用．考查了学生的观察思考能力．
练习册系列答案
阅读快车系列答案
相关题目
有一段演绎推理：“因为对数函数y=logax是减函数；已知y=log2x是对数函数，所以y=log2x是减函数”，结论显然是错误的，这是因为（ ）
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、非以上错误 |
为了得到函数y=sin（
x-
）的图象，只需将y=sin
x图象上的每个点纵坐标不变，横坐标（ ）
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知动点P（t，t），Q（10-t，0），其中0＜t＜10，则点M（6，1），N（4，5）与直线PQ的关系是（ ）
| A、M，N均在直线PQ上 |
| B、M，N均不在直线PQ上 |
| C、M不在直线PQ上，N可能在直线PQ上 |
| D、M可能在直线PQ上，N不在直线PQ上 |
下列选项中两个函数相同的是（ ）
A、y=x，y=
| ||||||
B、y=|x|，y=
| ||||||
| C、y=1，y=x0 | ||||||
D、y=
|
已知{an}为等差数列，{bn}为正项等比数列，公比q≠1，若a1=b1，a15=b15，则（ ）
| A、a8≥b8 |
| B、a8＞b8 |
| C、a8≤b8 |
| D、a8＜b8 |
已知实数x，y满足
，则目标函数z=x+2y的最大值为（ ）
|
| A、1 | ||
B、
| ||
| C、4 | ||
| D、5 |
已知向量
=（-1，x），
=（1，x），若2
-
与
垂直，则|a|=（ ）
| a |
| b |
| b |
| a |
| a |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |