题目内容
函数f(x)=x2-6x+8在[-1,5]上的最大值和最小值分别为( )
| A、15,3 | B、15,-1 |
| C、8,-1 | D、20,-4 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:先将解析式化为顶点式就可以求出最小值,再根据对称轴在其取值范围内就可以求出最大值.
解答:
解:∵f(x)=x2-6x+8(-1≤x≤2),
∴f(x)=(x-3)2-1,
∴抛物线的对称轴为x=3,当x=3时y有最小值:-1,
∵-1≤x≤5,
∴x=-1时,f(-1)=15是最大值.
∴函数的最大值为15,最小值为-1.
故选:B.
∴f(x)=(x-3)2-1,
∴抛物线的对称轴为x=3,当x=3时y有最小值:-1,
∵-1≤x≤5,
∴x=-1时,f(-1)=15是最大值.
∴函数的最大值为15,最小值为-1.
故选:B.
点评:本题是一道有关二次函数图象性质的题,考查了二次函数的顶点式和二次函数的最值的运用.

练习册系列答案
相关题目
椭圆
+
=1的离心率为
,则m=( )
| y2 |
| 16 |
| x2 |
| m |
| ||
| 2 |
| A、8 | ||||
| B、32 | ||||
| C、8或32 | ||||
D、2
|
已知函数f(x)是定义在区间[3a-5,2a]上的奇函数,则实数a的值为( )
| A、1 | ||
B、
| ||
| C、0 | ||
| D、不确定 |
若a、b是任意实数,且a>b,则下列不等式恒成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
D、(
|
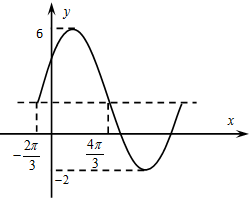 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<