题目内容
已知过抛物线y2=x的焦点F的直线m的倾斜角是θ≥
,m交抛物线于A,B两点且A在x轴上方,则|FA|的取值范围是 .
| π |
| 4 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:当倾斜角θ=
时,直线m的方程为:y=x-
,与抛物线方程联立可得16x2-24x+1=0,取x=
,由于π>θ≥
,可得0<xA≤
.利用|FA|=xA+
即可得出.
| π |
| 4 |
| 1 |
| 4 |
3+2
| ||
| 4 |
| π |
| 4 |
3+2
| ||
| 4 |
| 1 |
| 4 |
解答:
解:当倾斜角θ=
时,直线m的方程为:y=x-
,
联立
,化为16x2-24x+1=0,
解得x=
,
取x=
,
∵π>θ≥
,
∴0<xA≤
.
|FA|=xA+
.
∴
<|FA|≤1+
.
故答案为:(
,1+
].
| π |
| 4 |
| 1 |
| 4 |
联立
|
解得x=
3±2
| ||
| 4 |
取x=
3+2
| ||
| 4 |
∵π>θ≥
| π |
| 4 |
∴0<xA≤
3+2
| ||
| 4 |
|FA|=xA+
| 1 |
| 4 |
∴
| 1 |
| 4 |
| ||
| 2 |
故答案为:(
| 1 |
| 4 |
| ||
| 2 |
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立、焦点弦公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知i是虚数单位,集合M=N(整数集),集合N=(i,i2,i3,i4),则集合M∩N的元素共有( )
| A、3个 | B、2个 | C、1个 | D、无穷个 |
已知函数若f(x)=cosx-log
x,则f(x)在其定义域上零点的个数为( )
| 1 |
| 10 |
| A、1个 | B、3个 | C、5个 | D、7个 |
函数f(x)=ln(x+1)-
的零点所在的大致区间是( )
| 2 |
| x |
| A、(3,4) |
| B、(2,3) |
| C、(1,2) |
| D、(0,1) |
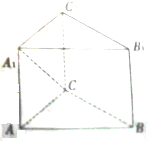 大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,
大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,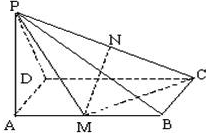 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.