题目内容
口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量X,求X的分布列和数学期望E(X).
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量X,求X的分布列和数学期望E(X).
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式,离散型随机变量及其分布列
专题:计算题,概率与统计
分析:(Ⅰ)记“恰有一个黑球”为事件A,则P(A)=
=
=
.
(Ⅱ)X的可能取值为0,1,2,则P(X=0)=
=
,P(X=1)=
=
=
,P(X=2)=P(A)=
,从而列分布列并求数学期望.
| ||||
|
| 4 |
| 20 |
| 1 |
| 5 |
(Ⅱ)X的可能取值为0,1,2,则P(X=0)=
| ||
|
| 1 |
| 5 |
| ||||
|
| 12 |
| 20 |
| 3 |
| 5 |
| 1 |
| 5 |
解答:
解:(Ⅰ)记“恰有一个黑球”为事件A,则
P(A)=
=
=
.
(Ⅱ)X的可能取值为0,1,2,则
P(X=0)=
=
,P(X=1)=
=
=
,P(X=2)=P(A)=
;
则X的分布列为
∴X的数学期望EX=0×
+1×
+2×
=1.
P(A)=
| ||||
|
| 4 |
| 20 |
| 1 |
| 5 |
(Ⅱ)X的可能取值为0,1,2,则
P(X=0)=
| ||
|
| 1 |
| 5 |
| ||||
|
| 12 |
| 20 |
| 3 |
| 5 |
| 1 |
| 5 |
则X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
点评:本题考查了概率的求法及分布列与数学期望的求法,属于基础题.

练习册系列答案
相关题目
已知f(x)=ax5+bx3+cx+1(a≠0),若f(2014)=m,则f(-2014)=( )
| A、-m | B、m | C、0 | D、2-m |
已知函数若f(x)=cosx-log
x,则f(x)在其定义域上零点的个数为( )
| 1 |
| 10 |
| A、1个 | B、3个 | C、5个 | D、7个 |
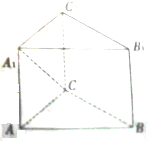 大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,
大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,