题目内容
在△ABC中,
=
,
=
,若
=
,
=2
,则
= .(用
,
表示)
| AB |
| a |
| AC |
| b |
| BC |
| DC |
| AE |
| EC |
| ED |
| a |
| b |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用沙尔定理直接将向量
写成
+
+
,再结合已知的条件将每个向量用
,
表示出来即可.
| ED |
| DB |
| BA |
| AE |
| a |
| b |
解答:
解:因为
=
,所以
=
=
(
-
)=
(
-
).
因为
=2
,所以
=
=
.
=-
=-
,
所以
=
+
+
,将上述结果代入前式得:
=
(
-
)-
+
=-
+
.
所以
=-
=
-
.
故答案为:
-
| BD |
| DC |
| DB |
| 1 |
| 2 |
| CB |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| a |
| b |
因为
| AE |
| EC |
| AE |
| 2 |
| 3 |
| AC |
| 2 |
| 3 |
| b |
| BA |
| AB |
| a |
所以
| DE |
| DB |
| BA |
| AE |
| DE |
| 1 |
| 2 |
| a |
| b |
| a |
| 2 |
| 3 |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 6 |
| b |
所以
| ED |
| DE |
| 1 |
| 2 |
| a |
| 1 |
| 6 |
| b |
故答案为:
| 1 |
| 2 |
| a |
| 1 |
| 6 |
| b |
点评:本题考查了平面向量加法、减法的几何意义以及数乘的运算.要注意向量间方向、模长间的关系.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
函数f(x)=ln(x+1)-
的零点所在的大致区间是( )
| 2 |
| x |
| A、(3,4) |
| B、(2,3) |
| C、(1,2) |
| D、(0,1) |
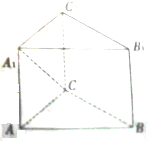 大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,
大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,