题目内容
某简谐运动的图象对应的函数解析式为:y=
sin(2x-
).
(1)指出此简谐运动的周期、振幅、频率、相位和初相;
(2)利用“五点法”作出函数在一个周期(闭区间)上的简图;
(3)说明它是由函数y=sinx的图象经过哪些变换而得到的.
【解】:(1)周期: ;振幅: ;频率: ;相位: ;初相: ;
(2)

(3)①先将函数y=sinx的图象 得到函数y=sin2x的图象;②再将函数y=sin2x的图象 得到函数y=sin(2x-
)的图象;③最后再将函数y=sin(2x-
)的图象 得到函数y=
sin(2x-
)的图象.
| 2 |
| π |
| 4 |
(1)指出此简谐运动的周期、振幅、频率、相位和初相;
(2)利用“五点法”作出函数在一个周期(闭区间)上的简图;
(3)说明它是由函数y=sinx的图象经过哪些变换而得到的.
【解】:(1)周期:
| x | |||||||
2x-
|
0 | ||||||
sin(2x-
|
|||||||
| y |

(3)①先将函数y=sinx的图象
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换,五点法作函数y=Asin(ωx+φ)的图象
专题:计算题,作图题,三角函数的图像与性质
分析:(1)利用函数的解析式直接求出周期、振幅、频率、相位、初相;
(2)题干列表,描点,连线画出函数一个周期内的函数的图象.
(3)利用三角函数的平移与伸缩变换左加右减的原则写出结果即可.
(2)题干列表,描点,连线画出函数一个周期内的函数的图象.
(3)利用三角函数的平移与伸缩变换左加右减的原则写出结果即可.
解答:
解:(1)周期:π;振幅:
;频率:
;相位:2x-
;初相:-
;(每空1分)
故答案为:周期:π;振幅:
;频率:
;相位:2x-
;初相:-
;
(2)图象如图(表格(2分),图象2分)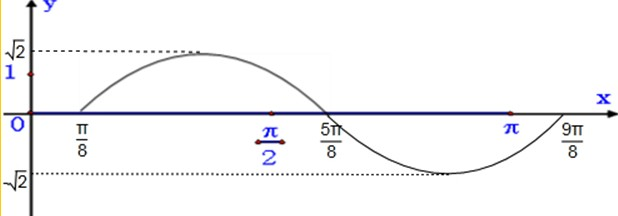
(3)①先将函数y=sinx的图象 上的点纵坐标不变横坐标缩短至原来的一半 得到函数y=sin2x的图象;
②再将函数y=sin2x的图象 右移
个单位得到函数y=sin(2x-
)的图象;
③最后再将函数y=sin(2x-
)的图象上的点横坐标不变纵坐标扩大至原来的
倍得到函数y=
sin(2x-
)的图象.(每空1分)
故答案为:上的点纵坐标不变横坐标缩短至原来的一半;右移
个单位;点横坐标不变纵坐标扩大至原来的
倍.
| 2 |
| 1 |
| π |
| π |
| 4 |
| π |
| 4 |
故答案为:周期:π;振幅:
| 2 |
| 1 |
| π |
| π |
| 4 |
| π |
| 4 |
(2)图象如图(表格(2分),图象2分)

| x |
|
|
|
|
| ||||||||||
2x-
|
0 |
|
π |
|
2π | ||||||||||
sin(2x-
|
0 | 1 | 0 | -1 | 0 | ||||||||||
| y | 0 |
|
0 | -
|
0 |
②再将函数y=sin2x的图象 右移
| π |
| 8 |
| π |
| 4 |
③最后再将函数y=sin(2x-
| π |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
故答案为:上的点纵坐标不变横坐标缩短至原来的一半;右移
| π |
| 8 |
| 2 |
点评:本题考查三角函数的图象与性质的应用,五点法画图,考查基本知识的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,已知角A=30°,a=8,b=8
,则△ABC的面积等于
( )
| 3 |
( )
A、32
| ||||
B、32
| ||||
C、32
| ||||
D、64
|
已知函数f(x)=
sin(2x+ϕ),若f(a)=
,则f(a+
)与f(a+
)的大小关系是( )
| 3 |
| 3 |
| 5π |
| 6 |
| π |
| 12 |
A、f(a+
| ||||
B、f(a+
| ||||
C、f(a+
| ||||
| D、大小与a、ϕ有关 |