已知$cosα=-\frac{3}{5}$.并且α是第二象限角.则tanα的值为( )A．$\frac{3}{4}$B．$-\frac{3}{4}$C．$\frac{4}{3}$D．$-\frac{4}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

16．已知$cosα=-\frac{3}{5}$，并且α是第二象限角，则tanα的值为（　　）

A．

$\frac{3}{4}$

B．

$-\frac{3}{4}$

C．

$\frac{4}{3}$

D．

$-\frac{4}{3}$

分析根据平方关系和α是第二象限角求出sinα，再根据商数关系求出tanα的值．

解答解：$cosα=-\frac{3}{5}$，且α是第二象限角，
∴sinα=$\sqrt{1{-cos}^{2}α}$=$\sqrt{1{-（-\frac{3}{5}）}^{2}}$=$\frac{4}{5}$，
∴tanα=$\frac{sinα}{cosα}$=$\frac{\frac{4}{5}}{-\frac{3}{5}}$=-$\frac{4}{3}$．
故选：D．

点评本题考查了同角的三角函数关系的应用问题，是基础题目．

练习册系列答案

中考总复习赢在中考系列答案

国华考试中考总动员系列答案

中国历史同步练习册系列答案

中考123基础章节总复习测试卷系列答案

相关题目

6．5人排成一列，其中甲、乙二人相邻的不同排法的种数为48．（结果用数字表示）

7．已知角α的终边过点（3，4）．
（Ⅰ）求sinα，cosα的值；
（Ⅱ）求$\frac{{2cos（{\frac{π}{2}-α}）-cos（{π+α}）}}{{2sin（{π-α}）}}$的值．

4．已知变量x，y满足$\left\{{\begin{array}{l}{x+2y-4≤0}\\{x≥1}\\{y≥0}\end{array}}\right.$，则z=-2x+y的最大值是（　　）

11．关于函数$f（x）=cos（2x-\frac{π}{3}）+cos（2x+\frac{π}{6}）$，则下列命题：
①y=f（x）的最大值为$\sqrt{2}$；
②y=f（x）在定义域上是偶函数；
③y=f（x）在区间$[\frac{π}{24}，\frac{13π}{24}]$上是减函数；
④将函数$y=\sqrt{2}cos2x$的图象向右平移$\frac{π}{24}$个单位后，将与函数y=f（x）的图象重合．
其中正确命题的序号是①③④．

1．抛物线y²=ax的准线方程是x=2，则a的值是（　　）

8．

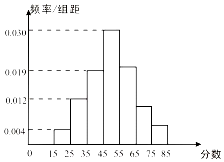某校1400名学生参加某次知识竞赛，从中随机抽取100名考生的成绩，绘制成如图所示的频率分布直方图，分数落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
（1）求这些分数落在区间[55，65）内的频率；
（2）估计该校参加本次知识竞赛中成绩低于45分的人数是多少？

5．《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为（　　）

6．已知{a_n}是等比数列，a₂=2且公比q＞0，-2，a₁，a₃成等差数列．
（Ⅰ）求q的值；
（Ⅱ）已知b_n=a_na_n+1-λna_n+1（n=1，2，3，…），设S_n是数列{b_n}的前n项和．若S₁＞S₂，且S_k＜S_k+1（k=2，3，4，…），求实数λ的取值范围．

试题分类