题目内容
8．
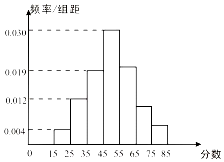某校1400名学生参加某次知识竞赛，从中随机抽取100名考生的成绩，绘制成如图所示的频率分布直方图，分数落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．（1）求这些分数落在区间[55，65）内的频率；
（2）估计该校参加本次知识竞赛中成绩低于45分的人数是多少？
分析 （1）设区间[75，85）内的频率为x，利用频率和为1，列出方程求出x的值，再求区间[55，65）内的频率；
（2）计算成绩低于45分的频率，从而求出对应的频数．
解答 解：（1）设区间[75，85）内的频率为x，
则区间[55，65），[65，75）内的频率分别为4x和2x．
依题意得（0.004+0.012+0.019+0.030）×10+4x+2x+x=1，
解得x=0.05，
所以区间[55，65）内的频率为0.2；
（2）由题意得成绩低于45分的频率为
0.04+0.12+0.19=0.35，
则成绩低于45分的人数约为
0.35×1400=490．
点评 本题考查了利用频率分布直方图计算频率与频数的应用问题，是基础题目．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
18．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{-x，x＜0}\end{array}\right.$，则f（f（-2））等于（ ）
| A． | 1 | B． | 2 | C． | $-\frac{1}{2}$ | D． | $\frac{1}{2}$ |
16．已知$cosα=-\frac{3}{5}$，并且α是第二象限角，则tanα的值为（ ）
| A． | $\frac{3}{4}$ | B． | $-\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $-\frac{4}{3}$ |
13．为大力提倡“厉行节约，反对浪费”，某市通过随机询问100名性别不同的居民是否做到“光盘”行动，得到如下列联表及附表：
经计算：${X^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}≈3.03$
参照附表，得到的正确结论是（ ）
经计算：${X^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}≈3.03$
| 做不到“光盘”行动 | 做到“光盘”行动 | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P（X2≥x0） | 0.10 | 0.05 | 0.025 |
| x0 | 2.706 | 3.841 | 5.024 |
| A． | 在犯错误的概率不超过1%的前提下，认为“该市民能否做到‘光盘’行动与性别有关” | |
| B． | 在犯错误的概率不超过1%的前提下，认为“该市民能否做到‘光盘’行动与性别无关” | |
| C． | 有90%以上的把握认为“该市民能否做到‘光盘’行动与性别有关” | |
| D． | 有90%以上的把握认为“该市民能否做到‘光盘’行动与性别无关” |
17．在△ABC中，角A，B，C所对的边分别为a，b，c，若$sinC=\frac{2}{3}，a=3，c=4$，则角A等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |