题目内容
到A（2，-3）和直线y=4距离相等的点的轨迹方程是 ．
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：设出动点坐标，由题意列等式，平方后整理得答案．
解答：
解：设动点为M（x，y），
由题意得：
=|x-4|，
两边平方并整理得：（y+3）2=-4（x-3）．
∴到A（2，-3）和直线y=4距离相等的点的轨迹方程是（y+3）2=-4（x-3）．
故答案为：（y+3）2=-4（x-3）．
由题意得：
| (x-2)2+(y+3)2 |
两边平方并整理得：（y+3）2=-4（x-3）．
∴到A（2，-3）和直线y=4距离相等的点的轨迹方程是（y+3）2=-4（x-3）．
故答案为：（y+3）2=-4（x-3）．
点评：本题考查了轨迹方程的求法，关键是由已知正确列出等式，是基础题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
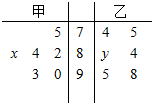如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩，已知甲同学的平均成绩为85，乙同学的六科成绩的众数为84，则x，y的值为（ ）| A、2，4 | B、4，4 |
| C、5，6 | D、6，4 |
两直线2x+3y-k=0和x+ky-12=0的交点在y轴上，那么k的值是（ ）
| A、-24 | B、6 | C、±6 | D、24 |