题目内容
19.在三棱锥S-ABC中,∠ACB=90°,SA⊥平面ABC,SA=2,AC=BC=1,则异面直线SB与AC所成角的余弦值是( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{6}$ |
分析 如图所示,把△ABC补成正方形EACB,则有AE∥BC,AC∥BE.即∠SBE就是异面直线SB与AC所成的角.解直角三角形SBE即可得到结果.
解答 解:如图所示,把△ABC补成正方形EACB,则有AE∥BC,AC∥BE.
∴∠SBE就是异面直线SB与AC所成的角.
∵∠ACB=90°,SA⊥平面ABC,可得BC⊥面SAC,AE⊥面SAC,
∵SA=2,AC=BC=1,∴$SE=\sqrt{{2}^{2}+{1}^{1}}=\sqrt{5}$
∵AC⊥AE,AC⊥SA,SA∩AE=A,∴AC⊥面SAE,
∴BE⊥面SAE,即BE⊥SE.
在Rt△SEB中,cos$∠SBE=\frac{BE}{SB}=\frac{\sqrt{6}}{6}$.
故选:D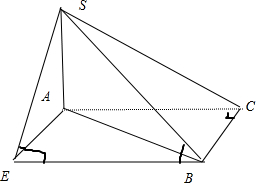
点评 本题考查了空间异面直线的夹角的计算,属于中档题.

练习册系列答案
相关题目
14.已知集合A={x|x≤1},B={x|x2-x≤0},则A∩B=( )
| A. | {x|x≤-1} | B. | {x|-1≤x≤0} | C. | {x|0≤x≤1} | D. | {x|1≤x≤2} |
4.等比数列{an}的前n项和为Sn,且4a1,2a2,a3成等差数列,若a1=1,则S10=( )
| A. | 512 | B. | 511 | C. | 1024 | D. | 1023 |
11.已知函数f(x)=2x-e2x(e为自然对数的底数),g(x)=mx+1,(m∈R),若对于任意的x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,则实数m的取值范围为( )
| A. | (-∞,1-e2]∪[e2-1,+∞) | B. | [1-e2,e2-1] | ||
| C. | (-∞,e-2-1]∪[1-e-2,+∞) | D. | [e-2-1,1-e-2] |
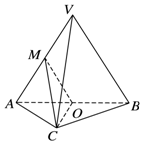 如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.
如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.