题目内容
已知向量
=（-1，x），
=（1，x），若2
-
与
垂直，则|a|=（ ）
| a |
| b |
| b |
| a |
| a |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的坐标运算、向量垂直与数量积的关系、模的计算公式即可得出．
解答：
解：∵向量
=（-1，x），
=（1，x），
∴2
-
=2（1，x）-（-1，x）=（3，x）．
∵2
-
与
垂直，
∴（2
-
）•
=-3+x2=0，解得x2=3．
∴|
|=
=2．
故选：C．
| a |
| b |
∴2
| b |
| a |
∵2
| b |
| a |
| a |
∴（2
| b |
| a |
| a |
∴|
| a |
| 1+x2 |
故选：C．
点评：本题考查了向量的坐标运算、向量垂直与数量积的关系、模的计算公式，属于基础题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
已知双曲线
-
=1（m＞0，n＞0）的离心率为2，有一个焦点与抛物线y2=16x的焦点重合，则mn的值为（ ）
| x2 |
| m |
| y2 |
| n |
| A、4 | B、12 | C、16 | D、48 |
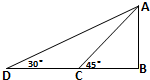如图，D，C，B在地平面同一直线上，DC=10m，从D，C两地测得A点的仰角分别为30°和45°，则A点离地面的高AB等于（ ）| A、10m | ||
B、5
| ||
C、5（
| ||
D、5（
|
已知实数x＞0，则下列不等式中不能恒成立的一个是（ ）
| A、lnx+1＜x＜ex-1 | ||
| B、sinx-x＜0 | ||
C、ex＞
| ||
| D、2x-x2≥0 |
f（sinx）=cos15x，则f（cosx）=（ ）
| A、sin15x |
| B、cos15x |
| C、-sin15x |
| D、-cos15x |
设f（x）=
，利用课本中推导等差数列前n项和的公式的方法，可求得：f（-12）+f（-11）+f（-10）+…+f（11）+f（12）+f（13）的值（ ）
| ||
3x+
|
| A、11 | B、14 | C、12 | D、13 |
利用归纳推理推断，当n是自然数时，
（n2-1）[1-（-1）n]的值（ ）
| 1 |
| 8 |
| A、一定是零 |
| B、不一定是整数 |
| C、一定是偶数 |
| D、是整数但不一定是偶数 |