题目内容
已知{an}为等差数列，{bn}为正项等比数列，公比q≠1，若a1=b1，a15=b15，则（ ）
| A、a8≥b8 |
| B、a8＞b8 |
| C、a8≤b8 |
| D、a8＜b8 |
考点：等差数列的通项公式,等比数列的通项公式
专题：等差数列与等比数列
分析：由已知条件推导出a8=
，b8=
，由基本不等式可知a8＞b8．
| a1+a15 |
| 2 |
| a1•a15 |
解答：
解：∵{an}为等差数列，
∴a8=
，
∵{bn}为正项等比数列，
∴b8=
，公比q≠1，
∵a1=b1，a15=b15，
∴b8=
，
由基本不等式可知a8＞b8，
故选B．
∴a8=
| a1+a15 |
| 2 |
∵{bn}为正项等比数列，
∴b8=
| b1b15 |
∵a1=b1，a15=b15，
∴b8=
| a1•a15 |
由基本不等式可知a8＞b8，
故选B．
点评：本题考查两数大小的比较，是基础题，解题时要认真审题，注意基本不等式性质的合理运用．
练习册系列答案
相关题目
设p：f（x）=ex+mx+1在（0，+∞）内单调递增，q：m≥0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知x，y∈R且
，则存在θ∈R，使得（x-4）cosθ+ysinθ+
=0的概率为（ ）
|
| 2 |
A、
| ||
B、
| ||
C、2-
| ||
D、1-
|
已知不等式|x+2|+|x|≤a的解集是空集，则实数a的取值范围是（ ）
| A、a＜2 | B、a≤2 |
| C、a＞2 | D、a≥2 |
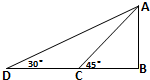如图，D，C，B在地平面同一直线上，DC=10m，从D，C两地测得A点的仰角分别为30°和45°，则A点离地面的高AB等于（ ）| A、10m | ||
B、5
| ||
C、5（
| ||
D、5（
|
已知实数x＞0，则下列不等式中不能恒成立的一个是（ ）
| A、lnx+1＜x＜ex-1 | ||
| B、sinx-x＜0 | ||
C、ex＞
| ||
| D、2x-x2≥0 |