题目内容
对某中学高二年级学生是爱好体育还是爱好文娱进行调查,共调查了40人,所得2×2列联表如下:
(1)将2×2列联表A、B、C、D、E三处补充完整;
(2)若已选出指定的三个男生甲、乙、丙,两个女生M,N,现从中选两人参加某项活动,求选出的两个人恰好是一男一女的概率;
(3)是否有85%的把握认为性别与爱好体育有关系?
附:K2=
参考数据:
| 爱好类型 性别 | 爱 好 体 育 | 爱 好 文 娱 | 合 计 |
| 男 生 | 15 | A | B |
| 女 生 | C | 10 | D |
| 合 计 | 20 | E | 40 |
(2)若已选出指定的三个男生甲、乙、丙,两个女生M,N,现从中选两人参加某项活动,求选出的两个人恰好是一男一女的概率;
(3)是否有85%的把握认为性别与爱好体育有关系?
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
参考数据:
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
考点:线性回归方程
专题:计算题,概率与统计
分析:(1)A为10,B为25,C为5,D为15,E为20.(2)利用古典概型概率公式求解即可,(3)求出K2的值查表即可.
解答:
解:(1)A为10,B为25,C为5,D为15,E为20.即:
(2)求选出的两个人恰好是一男一女的概率P=
=
=
.
(3)假设:性别与是否更喜欢体育没有关系.
K2=
=
=
≈2.6667>2.072,而P(K2≥2.072)=0.15,
∴有85%的把握可以认为性别与是否更喜欢体育有关系.
| 爱好类型 性别 | 爱 好 体 育 | 爱 好 文 娱 | 合 计 |
| 男 生 | 15 | 10 | 25 |
| 女 生 | 5 | 10 | 15 |
| 合 计 | 20 | 20 | 40 |
| ||||
|
| 6 |
| 10 |
| 3 |
| 5 |
(3)假设:性别与是否更喜欢体育没有关系.
K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 40×(15×10-5×10)2 |
| (15+10)(5+10)(15+5)(10+10) |
=
| 8 |
| 3 |
∴有85%的把握可以认为性别与是否更喜欢体育有关系.
点评:本题考查了2×2列联表的作法,及古典概型概率公式及独立性检验,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
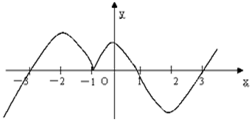 已知函数y=f(x)的导函数y=f′(x)图象如图所示
已知函数y=f(x)的导函数y=f′(x)图象如图所示