题目内容
在正方体ABCD-A1B1C1D1中，若过A、C、B1三点的平面与底面A1B1C1D1的交线为l，则l与A1C1的位置关系是 ．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由A1C1∥AC，得A1C1∥平面AB1C，平面AB1C∩底面A1B1C1D1=直线l，由线面平行的性质定理，得l∥A1C1．
解答：
解：因为A1C1∥AC，
A1C1不包含于平面AB1C，AC?平面AB1C，
所以A1C1∥平面AB1C，
又因为A1C1在底面A1B1C1D1内，
平面AB1C∩底面A1B1C1D1=直线l，
根据线面平行的性质定理，
得l∥A1C1．
故答案为：l∥A1C1．
A1C1不包含于平面AB1C，AC?平面AB1C，
所以A1C1∥平面AB1C，
又因为A1C1在底面A1B1C1D1内，
平面AB1C∩底面A1B1C1D1=直线l，
根据线面平行的性质定理，
得l∥A1C1．
故答案为：l∥A1C1．
点评：本题考查两直线的位置关系的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
在△ABC中，若
=
=
，则△ABC是（ ）
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、钝角三角形 |
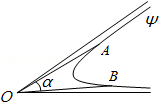如图，对于曲线Ψ所在平面内的点O，若存在以O为顶点的角α，使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立，则称角α为曲线Ψ的相对于点O的“界角”，并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”．已知曲线C：f（x）=
|
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中是偶函数且在（0，+∞）上单调递增的是（ ）
| A、y=2-x |
| B、y=lnx |
| C、y=x-2 |
| D、y=|x|-1 |
已知圆C：x2+（y-3）2=9，过原点作圆C的弦OP，则OP的中点Q的轨迹方程为（ ）
A、（x-
| ||||
B、（x-
| ||||
C、x2+（y-
| ||||
D、x2+（y-
|