题目内容
已知函数f(x)=x2-alnx在(1,2]上是增函数,g(x)=x-a
在(0,1)上为减函数,有以下四个结论:①a的取值有无数个;
②a的取值是唯一的;
③当x>0时,f(x)≥g(x)+2恒成立,当且仅当x=2时取等号;
④当b>-1时,若f(x)≥2bx-
在x∈(0,1]内恒成立,则b的取值范围是(-1,1].
其中正确的结论是( )
| x |
②a的取值是唯一的;
③当x>0时,f(x)≥g(x)+2恒成立,当且仅当x=2时取等号;
④当b>-1时,若f(x)≥2bx-
| 1 |
| x2 |
其中正确的结论是( )
| A、①③ | B、②③ | C、②④ | D、③④ |
考点:函数恒成立问题,函数单调性的性质
专题:综合题,导数的综合应用
分析:依题意f'(x)≥0,?x∈(1,2]恒成立,即a≤2x2,?x∈(1,2]恒成立,又g′(x)=1-
,依题意恒成立g'(x)≤0,?x∈(0,1),故①不正确;②正确;
由f(x)=g(x)+2知,方程x2-2lnx-x+2
-2=0,设h(x)=x2-2lnx-x+2
-2(x>0),确定h(x)在x=1处有一个最小值0,即可判断;
分离b得出b≤
-
+
,令φ(x)=
-
+
,需b≤φ(x)min.
| a | ||
2
|
由f(x)=g(x)+2知,方程x2-2lnx-x+2
| x |
| x |
分离b得出b≤
| x |
| 2 |
| lnx |
| x |
| 1 |
| 2x3 |
| x |
| 2 |
| lnx |
| x |
| 1 |
| 2x3 |
解答:
解:f′(x)=2x-
,
依题意f'(x)≥0,?x∈(1,2]恒成立,即a≤2x2,?x∈(1,2]恒成立.
∴a≤2(1)
又g′(x)=1-
,依题意,?x∈(0,1),g'(x)≤0恒成立,
即a≥2
,?x∈(0,1)恒成立.
∴a≥2.(2)
由(1)(2)得a=2.故①不正确;②正确;
由f(x)=g(x)+2知,方程x2-2lnx-x+2
-2=0,
设h(x)=x2-2lnx-x+2
-2(x>0),
则h′(x)=
,令h'(x)=0,并由x>0,得x=1.
列表分析:
知h(x)在x=1处有一个最小值0,
∴当x>0时,f(x)≥g(x)+2恒成立,当且仅当x=1时取等号,故③不正确;
(4)f(x)≥2bx-
,即x2-2lnx≥2bx-
在x∈(0,1]内恒成立,
分离b得出b≤
-
+
,令φ(x)=
-
+
,需b≤φ(x)min
求导得出φ′(x)=
-
-
.
由于x∈(0,1],所以 φ′(x)=
-
-
<0,
φ(x)在(0,1]上单调递减,φ(x)≥φ(1)=1,所以b≤1,又b>-1,所以1>b>-1,即④正确.
故选:C.
| a |
| x |
依题意f'(x)≥0,?x∈(1,2]恒成立,即a≤2x2,?x∈(1,2]恒成立.
∴a≤2(1)
又g′(x)=1-
| a | ||
2
|
即a≥2
| x |
∴a≥2.(2)
由(1)(2)得a=2.故①不正确;②正确;
由f(x)=g(x)+2知,方程x2-2lnx-x+2
| x |
设h(x)=x2-2lnx-x+2
| x |
则h′(x)=
(
| ||||
| x |
列表分析:
| x | (0,1) | 1 | (1,+∞) |
| h'(x) | - | 0 | + |
| h(x) | 递减 | 0 | 递增 |
∴当x>0时,f(x)≥g(x)+2恒成立,当且仅当x=1时取等号,故③不正确;
(4)f(x)≥2bx-
| 1 |
| x2 |
| 1 |
| x2 |
分离b得出b≤
| x |
| 2 |
| lnx |
| x |
| 1 |
| 2x3 |
| x |
| 2 |
| lnx |
| x |
| 1 |
| 2x3 |
求导得出φ′(x)=
| 1 |
| 2 |
| 3 |
| 2x4 |
| 1-lnx |
| x2 |
由于x∈(0,1],所以 φ′(x)=
| 1 |
| 2 |
| 3 |
| 2x4 |
| 1-lnx |
| x2 |
φ(x)在(0,1]上单调递减,φ(x)≥φ(1)=1,所以b≤1,又b>-1,所以1>b>-1,即④正确.
故选:C.
点评:本题考查导数在求函数最大值、最小值中的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大.

练习册系列答案
相关题目
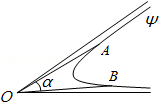 如图,对于曲线Ψ所在平面内的点O,若存在以O为顶点的角α,使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立,则称角α为曲线Ψ的相对于点O的“界角”,并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”.已知曲线C:f(x)=
如图,对于曲线Ψ所在平面内的点O,若存在以O为顶点的角α,使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立,则称角α为曲线Ψ的相对于点O的“界角”,并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”.已知曲线C:f(x)=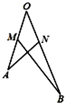 如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设
如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设