题目内容
10.已知函数f(x)=|2x+1|+|2x-3|.(Ⅰ)解方程f(x)-4=0;
(Ⅱ)若关于x的不等式f(x)≤a解集为空集,求实数a的取值范围.
分析 (Ⅰ)通过讨论x的范围,得到关于x的各个范围内的不等式组,解出取并集即可;
(Ⅱ)问题转化为a<f(x)min,根据绝对值的性质求出f(x)的最小值,从而求出a的范围即可.
解答 解:(Ⅰ)由$f(x)=|{2x+1}|+|{2x-3}|=\left\{\begin{array}{l}-4x+2({x<-\frac{1}{2}})\\ 4({-\frac{1}{2}≤x≤\frac{3}{2}})\\ 4x-2({x>\frac{3}{2}})\end{array}\right.$
∴原方程等价于$\left\{\begin{array}{l}x<-\frac{1}{2}\\-4x+2-4=0\end{array}\right.$或$\left\{\begin{array}{l}-\frac{1}{2}≤x≤\frac{3}{2}\\ 4-4=0\end{array}\right.$或$\left\{\begin{array}{l}x>\frac{3}{2}\\ 4x-2-4=0\end{array}\right.$
解得:Φ或$-\frac{1}{2}≤x≤\frac{3}{2}$或Φ
即方程f(x)-4=0的解为$\left\{{\left.x\right|-\frac{1}{2}≤x≤\frac{3}{2}}\right\}$
(Ⅱ)∵关于x的不等式f(x)≤a解集为空集,
∴a<f(x)min
又∵f(x)=|2x+1|+|2x-3|≥|2x+1|-|2x-3|=4
∴a<4.
点评 本题考查了解绝对值不等式问题,考查绝对值的性质以及转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.函数f(x)=x2-2lnx的单调减区间是( )
| A. | (0,1) | B. | (1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(0,1) |
18.式子a2$\sqrt{a{b}^{3}\sqrt{a{b}^{5}}}$化简正确的是( )
| A. | a${\;}^{\frac{11}{4}}$b${\;}^{\frac{11}{4}}$ | B. | a${\;}^{\frac{11}{4}}$b${\;}^{\frac{11}{2}}$ | C. | a${\;}^{\frac{11}{4}}$ | D. | b${\;}^{\frac{11}{4}}$ |
5.设a=ln2,b=log23,c=log3$\frac{1}{2}$,则a,b,c的大小关系是( )
| A. | a>c>b | B. | b>c>a | C. | b>a>c | D. | c>b>a |
8.椭圆$\frac{x^2}{{{m^2}+12}}+\frac{y^2}{{{m^2}-4}}$=1的焦距是( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 与m有关 |
9.下列各数中最小的数是( )
| A. | 111111(2) | B. | 1000(4) | C. | 210(6) | D. | 85(9) |
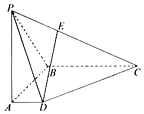 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.