题目内容
20.函数f(x)=x2-2lnx的单调减区间是( )| A. | (0,1) | B. | (1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(0,1) |
分析 依题意,可求得f′(x),由f′(x)<0即可求得函数f(x)=x2-2lnx的单调减区间.
解答 解:∵f(x)=x2-2lnx(x>0),
∴f′(x)=2x-$\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,
令f′(x)<0由图得:0<x<1,
∴函数f(x)=x2-2lnx的单调减区间是(0,1),
故选:A.
点评 本题考查利用导数研究函数的单调性,考查解不等式的能力,属于中档题.

练习册系列答案
相关题目
11.已知向量$|{\overrightarrow a}|=4,|{\overrightarrow b}|=8,\overrightarrow a$与$\overrightarrow b$的夹角为60°,则$|{2\overrightarrow a+\overrightarrow b}|$=( )
| A. | $8\sqrt{3}$ | B. | $6\sqrt{3}$ | C. | 5 | D. | $\sqrt{19}$ |
15.函数f(x)=x-lnx的单调递减区间是( )
| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (-∞,0)∪(1,+∞) |
12. 直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )
直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )
 直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )
直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )| A. | 6 | B. | 8 | C. | 7 | D. | 9 |
9.在等比数列 {an}中,a3+a5=20,a4=8,则a2+a6=( )
| A. | 188 | B. | 24 | C. | 32 | D. | 34 |
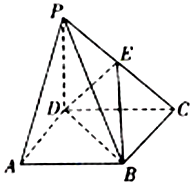 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PD⊥AB,PD⊥BC,且PD=1,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PD⊥AB,PD⊥BC,且PD=1,E为PC的中点.