题目内容
5．设a=ln2，b=log23，c=log3$\frac{1}{2}$，则a，b，c的大小关系是（ ）| A． | a＞c＞b | B． | b＞c＞a | C． | b＞a＞c | D． | c＞b＞a |
分析 利用指数函数、对数函数的单调性求解．
解答 解：∵0＜ln1＜a=ln2＜lne=1，
1=log22＜b=log23＜log24=2，
c=log3$\frac{1}{2}$＜log31=0，
∴a，b，c的大小关系为b＞a＞c．
故选：C．
点评 本题考查三个数的大小的求法，是基础题，解题时要认真审题，注意指数函数、对数函数的单调性的合理运用．
练习册系列答案
相关题目
15．函数f（x）=x-lnx的单调递减区间是（ ）
| A． | （0，1） | B． | （0，+∞） | C． | （1，+∞） | D． | （-∞，0）∪（1，+∞） |
13．已知x，y为正实数，则$\frac{4x}{x+3y}+\frac{3y}{x}$的最小值为（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{10}{3}$ | C． | $\frac{3}{2}$ | D． | 3 |
17．将函数$f（x）=2sin（{2x+\frac{π}{6}}）$的图象向左平移$\frac{π}{12}$个单位，再向上平移1个单位，得到g（x）的图象．若g（x1）g（x2）=9，且x1，x2∈[-2π，2π]，则2x1-x2的最大值为（ ）
| A． | $\frac{49π}{12}$ | B． | $\frac{35π}{6}$ | C． | $\frac{25π}{6}$ | D． | $\frac{17π}{4}$ |
设函数f（x）=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$（a＞b＞0）的图象是曲线C．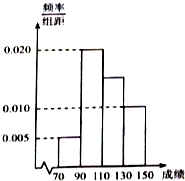
某班一次数学考试成绩频率分布直方图如图所示，数据分组依次为[70，90），[90，110），[110，130），[130，150]，已知成绩大于等于90分的人数为36人，现采用分层抽样的方式抽取一个容量为10的样本．