题目内容
2.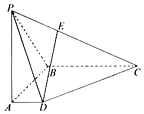 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.( I)设点E在线段PC上,若$\frac{PE}{EC}=\frac{1}{2}$,求证:DE∥平面PAB;
( II)求证:平面PBC⊥平面PAB.
分析 (Ⅰ)在PB上取一点F,满足$\frac{PF}{FB}=\frac{1}{2}$,连接EF,AF,可得EF∥BC,且$EF=\frac{1}{3}BC$,又AD∥BC,BC=3,AD=1,可得四边形ADEF为平行四边形,得DE∥AF,由线面平行的判定可得DE∥平面PAB;
(Ⅱ)由AD∥BC,∠DAB=90°,可得BC⊥AB,再由PA⊥底面ABCD,得BC⊥PA,由线面垂直的判定可得BC⊥平面PAB,进一步可得平面PBC⊥平面PAB.
解答 证明:(Ⅰ)∵$\frac{PE}{EC}=\frac{1}{2}$,∴在PB上取一点F,满足$\frac{PF}{FB}=\frac{1}{2}$,并连接EF,AF,
∵$\frac{PE}{EC}=\frac{PF}{FB}=\frac{1}{2}$,∴EF∥BC,且$EF=\frac{1}{3}BC$,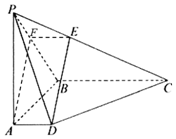
又AD∥BC,BC=3,AD=1,
∴EF∥AD,且EF=AD=1,
∴四边形ADEF为平行四边形,得DE∥AF,
又DE?面PAB,AF?面PAB,
∴DE∥平面PAB;
(Ⅱ)∵AD∥BC,∠DAB=90°,∴∠ABC=90°,即BC⊥AB,
又PA⊥底面ABCD,BC?底面ABCD,∴BC⊥PA,
又AB,PA是平面PAB上两相交直线,
∴BC⊥平面PAB,
又BC?平面PBC,∴平面PBC⊥平面PAB.
点评 本题考查直线与平面平行、平面与平面垂直的判定,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )
直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )
 直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )
直线y=x-1与圆$x_{\;}^2+y_{\;}^2-2x+\frac{3}{4}=0$及抛物线$y_{\;}^2=4x$依次交于A,B,C,D四点,则|AB|+|CD|=( )| A. | 6 | B. | 8 | C. | 7 | D. | 9 |
13.已知x,y为正实数,则$\frac{4x}{x+3y}+\frac{3y}{x}$的最小值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
17.将函数$f(x)=2sin({2x+\frac{π}{6}})$的图象向左平移$\frac{π}{12}$个单位,再向上平移1个单位,得到g(x)的图象.若g(x1)g(x2)=9,且x1,x2∈[-2π,2π],则2x1-x2的最大值为( )
| A. | $\frac{49π}{12}$ | B. | $\frac{35π}{6}$ | C. | $\frac{25π}{6}$ | D. | $\frac{17π}{4}$ |
1.函数y=log2(x-x2)的定义域为( )
| A. | (0,1) | B. | (-1,0) | C. | (1,+∞) | D. | (-∞,0) |
 设函数f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的图象是曲线C.
设函数f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的图象是曲线C.