题目内容
已知函数y=(1-k)x2+2x+1(k∈R),当k取何值时,该函数存在零点,求出零点.
考点:函数零点的判定定理
专题:函数的性质及应用
分析:分别讨论①k=1时,②k≠1时的情况,再分别求出k的范围和x的值即可.
解答:
解:①k=1时,y=2x+1,存在零点x=-
,
②k≠1时,y=(1-k)x2+2x+1为二次函数,
由题意得:△=4-4(1-k)=4k≥0,
解得:k≥0,
∴x=
=
,
| 1 |
| 2 |
②k≠1时,y=(1-k)x2+2x+1为二次函数,
由题意得:△=4-4(1-k)=4k≥0,
解得:k≥0,
∴x=
-2±2
| ||
| 2(1-k) |
-1±
| ||
| 1-k |
点评:本题考察了函数的零点问题,一次函数,二次函数的性质问题,是一道基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

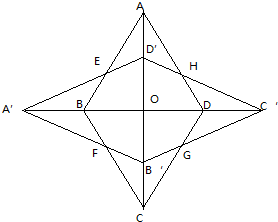 如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.
如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.