题目内容
17.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=3,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$.分析 由题意利用两个向量的数量积的定义求得$\overrightarrow{a}•\overrightarrow{b}$的值,再利用求向量的模方法计算求得结果.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=3,
∴$\overrightarrow{a}•\overrightarrow{b}$=1•3•cos$\frac{2π}{3}$=-$\frac{3}{2}$,
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{1-3+9}$=$\sqrt{7}$,
故答案为:$\sqrt{7}$.
点评 本题主要考查两个向量的数量积的定义、求向量的模,属于基础题.

练习册系列答案
相关题目
7.如图的框图是一古代数学家的一个算法的程序框图,它输出的结果S表示( )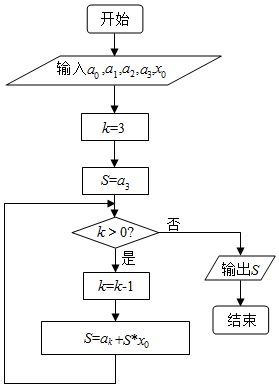

| A. | a0+a1+a2+a3的值 | B. | a3+a2x0+a1x02+a0x03的值 | ||
| C. | a0+a1x0+a2x02+a3x03的值 | D. | 以上都不对 |
5.在△ABC中,$\overrightarrow{CB}$•$\overrightarrow{CA}$=6,$\overrightarrow{BC}$•$\overrightarrow{BA}$=7,那么BC=( )
| A. | 13 | B. | 6 | C. | 7 | D. | $\sqrt{13}$ |
7.直线l过点A(3,4),且与点B(1,6)的距离最远,则直线l的方程为( )
| A. | x-y+1=0 | B. | x+y+1=0 | C. | x+y-7=0 | D. | x-y-7=0 |