题目内容
某公司有甲乙两个工作部门，假日去不同景点旅游，总共有m人参加，甲部门平均每人花费120元，乙部门每人花费110元，该公司去旅游的总共花去2250元，问甲乙两部门各去了多少人？
考点：根据实际问题选择函数类型
专题：函数的性质及应用
分析：根据甲乙两部门的平均费用，判断m的取值，然后设变量，建立方程关系即可得到结论．
解答：
解：设∵甲部门平均每人花费120元，乙部门每人花费110元，
∴
=18.75，
≈20.45，
∴总人数m，满足19≤m≤20，
若m=19，设甲部门有x人，则乙部门有19-x，
则得120x+（19-x）×110=2250，
解得x=16，即甲部门去了16人，乙部门去了3人．
若m=20，设甲部门有x人，则乙部门有20-x，
则得120x+（20-x）×110=2250，
解得x=5，即甲部门去了5人，乙部门去了15人．
∴
| 2250 |
| 120 |
| 2250 |
| 110 |
∴总人数m，满足19≤m≤20，
若m=19，设甲部门有x人，则乙部门有19-x，
则得120x+（19-x）×110=2250，
解得x=16，即甲部门去了16人，乙部门去了3人．
若m=20，设甲部门有x人，则乙部门有20-x，
则得120x+（20-x）×110=2250，
解得x=5，即甲部门去了5人，乙部门去了15人．
点评：本题主要考查函数的应用，根据条件确定人数m的取值，然后建立方程是解决本题的关键．
练习册系列答案
相关题目
如图所示．△ABC中，∠B=90°，M为AB上一点，使得AM=BC，N为BC上一点，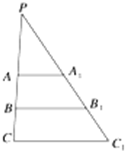
棱台的上底面积为16，下底面积为64，求棱台被它的中截面分成的上、下两部分体积之比．
如图：长方体ABCD-A1B1C1D1中，AB=3，AD=AA1=2，E为AB上一点，且AE=2EB，F为CC1的中点，P为C1D1上动点，当EF⊥CP时，PC1=