题目内容
设n∈N*且n≥2,证明:(a1+a2+…+an)2=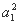
+
+…+
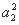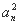+2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
(1) 当n=2时,有(a1+a2)2=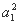++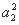2a1a2,命题成立.
(2) 假设当n=k(k≥2)时,命题成立,
即(a1+a2+…+ak)2=++…+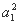
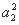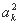+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立;
那么,当n=k+1时,有(a1+a2+…+ak+ak+1)2=(a1+a2+…+ak)2+2(a1+a2+…+ak)ak+1+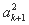
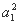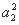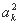=++…++2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…+ak)ak+1+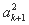=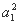++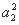…+++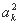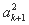2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1],
所以当n=k+1时,命题也成立.
根据(1)和(2),可知命题对任意的n∈N*且n≥2都成立.
练习册系列答案
相关题目
ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证: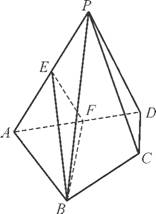
= . 
=4a1,则
+
的最小值为 .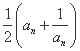 
.
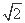,则圆C的标准方程为 . 
y2的焦点坐标为 .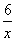 
∈N}是有限集．其中正确命题的个数是( )