题目内容
已知正项数列{an}满足Sn=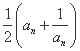 .
.
(1) 求a1,a2,a3并推测an;
(2) 用数学归纳法证明你的结论.
(1) 由Sn=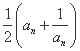 知
知
当n≥2时,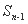 =
= ,
,
所以an=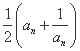 -
- ,
,
整理得an-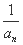 =-
=-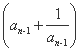 .
.
由S1=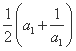 ,即a1=
,即a1=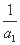 ,又a1>0,所以a1=1.
,又a1>0,所以a1=1.
a2- =-
=-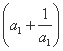 =-(1+1)=-2,即
=-(1+1)=-2,即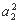 +2a2+1=2.
+2a2+1=2.
所以a2= -1,a3-
-1,a3- =-
=- =-
=-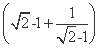 =-2
=-2 ,即
,即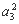 +2
+2 a3+2=3,
a3+2=3,
所以a3=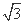 -
- ,可推测an=
,可推测an=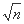 -
- .
.
(2) ①由(1)知a1=1,满足a1= -
-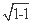 =1,
=1,
故当n=1时,an=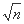 -
- 成立.
成立.
②假设n=k时,ak= -
-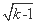 成立.
成立.
当n=k+1时,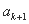 -
-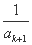 =-
=-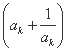 =-2
=-2 ,
,
即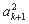 +2
+2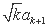 +k=k+1,所以
+k=k+1,所以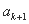 =
=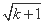 -
- ,即当n=k+1时,an=
,即当n=k+1时,an=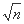 -
- .
.
由①②知数列{an}的通项公式为an=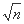 -
- ,n∈N*.
,n∈N*.

练习册系列答案
相关题目
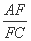 的值.
的值.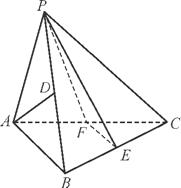
 中,a1=1,a2=2,且an+2=an+1+(-1)n(n∈N*),则S100= .
中,a1=1,a2=2,且an+2=an+1+(-1)n(n∈N*),则S100= . 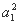 +
+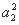 +…+
+…+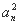 +2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
+2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].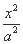 +
+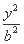 =1的焦点在x轴上,过点
=1的焦点在x轴上,过点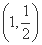 作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的方程是 .
作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的方程是 .